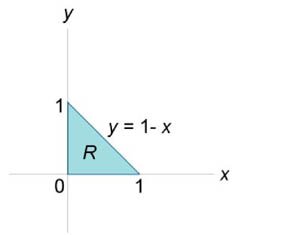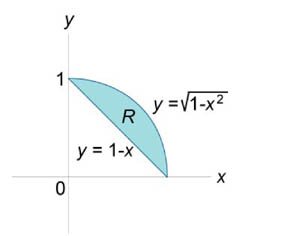Геометрические приложения двойных интегралов

Если \(f\left( {x,y} \right) = 1\) в интеграле \(\iint\limits_R {f\left( {x,y} \right)dxdy},\) то двойной интеграл равен площади области интегрирования \(R.\)

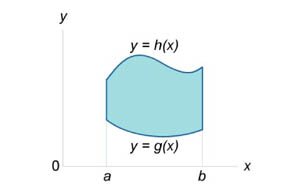
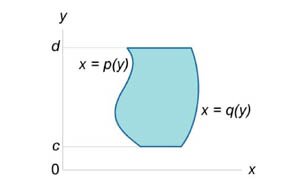
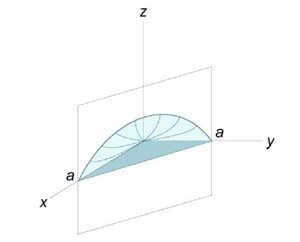
Площадь области типа \(I\) (элементарной относительно оси \(Oy\)) (рисунок \(1\)) выражается через повторный интеграл в виде \[A = \int\limits_a^b {\int\limits_{g\left( x \right)}^{h\left( x \right)} {dydx} } .\] Аналогично, площадь области типа \(II\) (элементарной относительно оси \(Ox\)) (рисунок \(2\)) описывается формулой \[A = \int\limits_c^d {\int\limits_{p\left( y \right)}^{q\left( y \right)} {dxdy} } .\] Если \({f\left( {x,y} \right)} > 0\) в области интегрирования \(R,\) то объем цилиндрического тела с основанием \(R,\) ограниченного сверху поверхностью \(z = {f\left( {x,y} \right)},\) выражается формулой \[V = \iint\limits_R {f\left( {x,y} \right)dA}.\] В случае, когда \(R\) является областью типа \(I,\) ограниченной линиями \(x = a,\) \(x = b,\) \(y = g\left( x \right),\) \(y = h\left( x \right),\) объем тела равен \[ {V = \iint\limits_R {f\left( {x,y} \right)dA} } = {\int\limits_a^b {\int\limits_{g\left( x \right)}^{h\left( x \right)} {f\left( {x,y} \right)dydx} } .} \] Для области \(R\) типа \(II,\) ограниченной графиками функций \(y = c,\) \(y = d,\) \(x = p\left( y \right),\) \(x = q\left( y \right),\) объем соответственно равен \[ {V = \iint\limits_R {f\left( {x,y} \right)dA} } = {\int\limits_c^d {\int\limits_{p\left( y \right)}^{q\left( y \right)} {f\left( {x,y} \right)dxdy} } .} \] Если в области \(R\) выполняется неравенство \(f\left( {x,y} \right) \ge g\left( {x,y} \right),\) то объем цилиндрического тела между поверхностями \({z_1} = g\left( {x,y} \right)\) и \({z_2} = f\left( {x,y} \right)\) с основанием \(R\) равен \[V = \iint\limits_R {\left[ {f\left( {x,y} \right) - g\left( {x,y} \right)} \right]dA}.\] Предположим, что поверхность задана функцией \(z = g\left( {x,y} \right),\) имеющей область определения \(R.\) Тогда площадь такой поверхности над областью \(R\) определяется формулой \[S = \iint\limits_R {\sqrt {1 + {{\left( {\frac{{\partial z}}{{\partial x}}} \right)}^2} + {{\left( {\frac{{\partial z}}{{\partial y}}} \right)}^2}} dxdy} \] при условии, что частные производные \({\large\frac{{\partial z}}{{\partial x}}\normalsize}\) и \({\large\frac{{\partial z}}{{\partial y}}\normalsize}\) непрерывны всюду в области \(R.\)

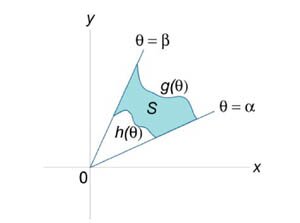
Пусть \(S\) является областью, ограниченной линиями \(\theta = \alpha,\) \(\theta = \beta,\) \(r = h\left( \theta \right),\) \(r = g\left( \theta \right)\) (рисунок \(3\)). Тогда площадь этой области определяется формулой \[ {A = \iint\limits_R {dA} } = {\int\limits_\alpha ^\beta {\int\limits_{h\left( \theta \right)}^{g\left( \theta \right)} {rdrd\theta } } .} \] Объем тела, ограниченного сверху поверхностью \(z = f\left( {r,\theta } \right)\) с основанием \(S,\) выражается в полярных координатах в виде \[V = \iint\limits_S {f\left( {r,\theta } \right)rdrd\theta } .\]

   Пример 1

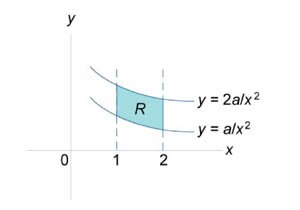
Найти площадь области \(R,\) ограниченной гиперболами \(y = \large\frac{{{a^2}}}{x}\normalsize,\;y = \large\frac{{2{a^2}}}{x}\normalsize\;\left( {a > 0} \right)\) и вертикальными прямыми \(x = 1,\) \(x = 2.\) Область \(R\) схематически показана на рисунке \(4.\) Используя формулу для площади области \(I\) типа \[ {A = \iint\limits_R {dxdy} } = {\int\limits_a^b {\int\limits_{g\left( x \right)}^{h\left( x \right)} {dydx} }, } \] получаем \[ {A = \iint\limits_R {dxdy} } = {\int\limits_1^2 {\left[ {\int\limits_{\frac{{{a^2}}}{x}}^{\frac{{2{a^2}}}{x}} {dy} } \right]dx} } = {\int\limits_1^2 {\left[ {\left. y \right|_{\frac{{{a^2}}}{x}}^{\frac{{2{a^2}}}{x}}} \right]dx} } = {\int\limits_1^2 {\left( {\frac{{2{a^2}}}{x} - \frac{{{a^2}}}{x}} \right)dx} } = {{a^2}\int\limits_1^2 {\frac{{dx}}{x}} } = {{a^2}\left( {\ln 2 - \ln 1} \right) = {a^2}\ln 2.} \]

   Пример 2

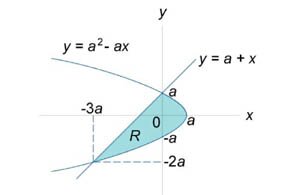
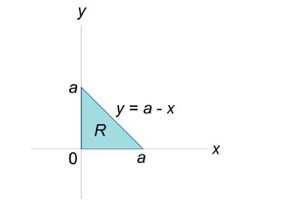
Вычислить площадь области \(R,\) ограниченной линиями \({y^2} = {a^2} - ax,\) \(y = a + x.\) Сначала определим точки пересечения двух заданных линий. \[ {\left\{ \begin{array}{l} {y^2} = {a^2} - ax\\ y = a + x \end{array} \right.,}\;\; {\Rightarrow {\left( {a + x} \right)^2} = {a^2} - ax,}\;\; {\Rightarrow {a^2} + 2ax + {x^2} = {a^2} - ax,}\;\; {\Rightarrow {x^2} + 3ax = 0,}\;\; {\Rightarrow x\left( {x + 3a} \right) = 0,}\;\; {\Rightarrow {x_{1,2}} = 0;\; - 3a.} \] Следовательно, координаты точек пересечения равны \[{x_1} = 0,\;\;{y_1} = a + 0 = a,\] \[{x_2} = - 3a,\;\;{y_2} = a - 3a = - 2a.\] Область \(R\) представлена на рисунке \(5.\) Будем рассматривать ее как область типа \(II.\) Для вычисления площади преобразуем уравнения границ: \[ {{y^2} = {a^2} - ax,}\;\; {\Rightarrow ax = {a^2} - {y^2},}\;\; {\Rightarrow x = a - \frac{{{y^2}}}{a},} \] \[ {y = a + x,}\;\; {\Rightarrow x = y - a.} \] Получаем \[ {A = \iint\limits_R {dxdy} } = {\int\limits_{ - 2a}^a {\left[ {\int\limits_{y - a}^{a - \frac{{{y^2}}}{a}} {dx} } \right]dy} } = {\int\limits_{ - 2a}^a {\left[ {\int\limits_{y - a}^{a - \frac{{{y^2}}}{a}} {dx} } \right]dy} } = {\int\limits_{ - 2a}^a {\left[ {\left. x \right|_{y - a}^{a - \frac{{{y^2}}}{a}}} \right]dy} } = {\int\limits_{ - 2a}^a {\left[ {a - \frac{{{y^2}}}{a} - \left( {y - a} \right)} \right]dy} } = {\int\limits_{ - 2a}^a {\left( {2a - \frac{{{y^2}}}{a} - y} \right)dy} } = {\left. {\left( {2ay - \frac{{{y^3}}}{{3a}} - \frac{{{y^2}}}{2}} \right)} \right|_{ - 2a}^a } = {\left( {2{a^2} - \frac{{{a^3}}}{{3a}} - \frac{{{a^2}}}{2}} \right) - \left( { - 4{a^2} + \frac{{8{a^3}}}{{3a}} - \frac{{4{a^2}}}{2}} \right) } = {\frac{{9{a^2}}}{2}.} \]

   Пример 3

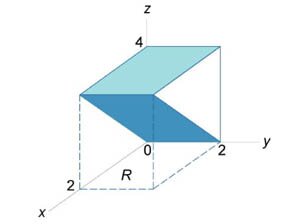
Найти объем тела в первом октанте, ограниченного плоскостями \(y = 0,\) \(z = 0,\) \(z = x,\) \(z + x = 4.\) Данное тело показано на рисунке \(6.\) Из рисунка видно, что основание \(R\) является квадратом. Для заданных \(x, y\) значение \(z\) изменяется от \(z = x\) до \(z = 4 - x.\) Тогда объем равен \[ {V = \iint\limits_R {\left[ {\left( {4 - x} \right) - x} \right]dxdy} } = {\int\limits_0^2 {\left[ {\int\limits_0^2 {\left( {4 - 2x} \right)dy} } \right]dx} } = {\int\limits_0^2 {\left[ {\left. {\left( {4y - 2xy} \right)} \right|_{y = 0}^2} \right]dx} } = {\int\limits_0^2 {\left( {8 - 4x} \right)dx} } = {\left. {\left( {8x - 2{x^2}} \right)} \right|_0^2 } = {16 - 8 = 8.} \]

   Пример 4

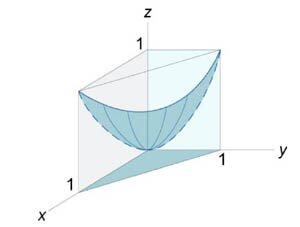
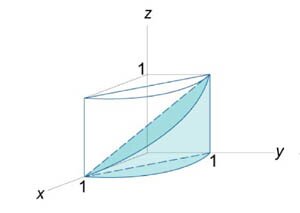
Описать тело, объем которого определяется интегралом \(V = \int\limits_0^1 {dx} \int\limits_0^{1 - x} {\left( {{x^2} + {y^2}} \right)dy} .\) Данное тело (рис.\(7,8\)) расположено над треугольной областью \(R,\) ограниченной координатными осями \(Ox,\) \(Oy\) и прямой \(y = 1 - x\) ниже параболической поверхности \(z = {x^2} + {y^2}.\) Объем тела равен \[ {V = \int\limits_0^1 {dx} \int\limits_0^{1 - x} {\left( {{x^2} + {y^2}} \right)dy} } = {\int\limits_0^1 {\left[ {\left. {\left( {{x^2}y + \frac{{{y^3}}}{3}} \right)} \right|_{y = 0}^{1 - x}} \right]dx} } = {\int\limits_0^1 {\left[ {{x^2}\left( {1 - x} \right) + \frac{{{{\left( {1 - x} \right)}^3}}}{3}} \right]dx} } = {\int\limits_0^1 {\left( {{x^2} - {x^3} + \frac{{1 - 3x + 3{x^2} - {x^3}}}{3}} \right)dx} } = {\int\limits_0^1 {\left( {2{x^2} - \frac{{4{x^3}}}{3} - x + \frac{1}{3}} \right)dx} } = {\left. {\left( {\frac{{2{x^3}}}{3} - \frac{4}{3} \cdot \frac{{{x^4}}}{4} - \frac{{{x^2}}}{2} + \frac{x}{3}} \right)} \right|_0^1 } = {\frac{2}{3} - \frac{1}{3} - \frac{1}{2} + \frac{1}{3} = \frac{1}{6}.} \]

   Пример 5

Вычислить объем тела, ограниченного поверхностями \(z = xy,\) \(x + y = a,\) \(z = 0.\) Данное тело лежит над треугольником \(R\) в плоскости \(Oxy\) (рисунки \(9,10\)) ниже поверхности \(z = xy.\) Объем тела равен \[ {V = \iint\limits_R {xydxdy} } = {\int\limits_0^a {\left[ {\int\limits_0^{a - x} {xydy} } \right]dx} } = {\int\limits_0^a {\left[ {\left. {\left( {\frac{{x{y^2}}}{2}} \right)} \right|_{y = 0}^{a - x}} \right]dx} } = {\frac{1}{2}\int\limits_0^a {x{{\left( {a - x} \right)}^2}dx} } = {\frac{1}{2}\int\limits_0^a {x\left( {{a^2} - 2ax + {x^2}} \right)dx} } = {\frac{1}{2}\int\limits_0^a {\left( {{a^2}x - 2a{x^2} + {x^3}} \right)dx} } = {\frac{1}{2}\left. {\left( {{a^2} \cdot \frac{{{x^2}}}{2} - 2a \cdot \frac{{{x^3}}}{3} + \frac{{{x^4}}}{4}} \right)} \right|_0^a } = {\frac{1}{2}\left( {\frac{{{a^2}}}{2} - \frac{{2{a^4}}}{3} + \frac{{{a^4}}}{4}} \right) } = {\frac{{{a^4}}}{{24}}.} \]

   Пример 6

Найти объем тела, ограниченного поверхностями \(z = 0,\) \(x + y = 1,\) \({x^2} + {y^2} = 1,\) \(z = 1 - x.\) Как видно из рисунков \(11\) и \(12,\) в области интегрирования \(R\) при \(0 \le x \le 1\) значения \(y\) изменяются от \(1 - x\) до \(\sqrt {1 - {x^2}}.\) Сверху тело ограничено плоскостью \(z = 1 - x.\) Следовательно, объем данного тела равен \[ {V = \iint\limits_R {\left( {1 - x} \right)dxdy} } = {\int\limits_0^1 {\left[ {\int\limits_{1 - x}^{\sqrt {1 - {x^2}} } {\left( {1 - x} \right)dy} } \right]dx} } = {\int\limits_0^1 {\left[ {\left( {1 - x} \right)\left. y \right|_{1 - x}^{\sqrt {1 - {x^2}} }} \right]dx} } = {\int\limits_0^1 {\left( {1 - x} \right)\left( {\sqrt {1 - {x^2}} - 1 + x} \right)dx} } = {\int\limits_0^1 {\left( {\sqrt {1 - {x^2}} - x\sqrt {1 - {x^2}} - 1 + 2x - {x^2}} \right)dx} } = {\int\limits_0^1 {\sqrt {1 - {x^2}} dx} } - {\int\limits_0^1 {x\sqrt {1 - {x^2}} dx} } - {\int\limits_0^1 {\left( {1 + 2x - {x^2}} \right)dx} .} \] Вычислим полученные три интеграла отдельно. \[{I_1} = \int\limits_0^1 {\sqrt {1 - {x^2}} dx} .\] Сделаем замену: \(x = \sin t.\) Тогда \(dx = \cos tdt.\) Видно, что \(t = 0\) при \(x = 0\) и \(t = \large\frac{\pi }{2}\normalsize\) при \(x = 1.\) Следовательно, \[ {{I_1} = \int\limits_0^1 {\sqrt {1 - {x^2}} dx} } = {\int\limits_0^{\large\frac{\pi }{2}\normalsize} {\sqrt {1 - {{\sin }^2}t} \cos tdt} } = {\int\limits_0^{\large\frac{\pi }{2}\normalsize} {{{\cos }^2}tdt} } = {\int\limits_0^{\large\frac{\pi }{2}\normalsize} {\frac{{1 + \cos 2t}}{2}dt} } = {\frac{1}{2}\int\limits_0^{\large\frac{\pi }{2}\normalsize} {\left( {1 + \cos 2t} \right)dt} } = {\frac{1}{2}\left. {\left( {t + \frac{{\sin 2t}}{2}} \right)} \right|_0^{\large\frac{\pi }{2}\normalsize} } = {\frac{1}{2}\left( {\frac{\pi }{2} + \frac{{\sin \pi }}{2}} \right) = \frac{\pi }{4}.} \] (Сравните с площадью сектора единичного круга в первом квадранте).

Вычислим второй интеграл \({I_2} = \int\limits_0^1 {x\sqrt {1 - {x^2}} dx},\) используя замену переменной. Полагаем \(1 - {x^2} = w.\) Тогда \(-2xdx = dw\) или \(xdx = \large\frac{{ - dw}}{2}\normalsize.\) Находим, что \(w = 1\) при \(x = 0\) и, наоборот, \(w = 0\) при \(x = 1.\) Интеграл равен \[ {{I_2} = \int\limits_0^1 {x\sqrt {1 - {x^2}} dx} } = {\int\limits_1^0 {\sqrt w \left( { - \frac{{dw}}{2}} \right)} } = { - \frac{1}{2}\int\limits_1^0 {\sqrt w dw} } = {\frac{1}{2}\int\limits_0^1 {\sqrt w dw} } = {\frac{1}{2}\int\limits_0^1 {{w^{\large\frac{1}{2}\normalsize}}dw} } = {\frac{1}{2}\left. {\left( {\frac{{2{w^{\large\frac{3}{2}\normalsize}}}}{3}} \right)} \right|_0^1 = \frac{1}{3}.} \] Наконец, вычислим третий интеграл. \[\require{cancel} {{I_3} = \int\limits_0^1 {\left( {1 - 2x + {x^2}} \right)dx} } = {\left. {\left( {x - {x^2} + \frac{{{x^3}}}{3}} \right)} \right|_0^1 } = {\cancel{1} - \cancel{1} + \frac{1}{3} = \frac{1}{3}.} \] Таким образом, объем тела равен \[ {V = {I_1} - {I_2} - {I_3} } = {\frac{\pi }{4} - \frac{1}{3} - \frac{1}{3} = \frac{\pi }{4} - \frac{2}{3} \approx 0,12.} \]

   Пример 7

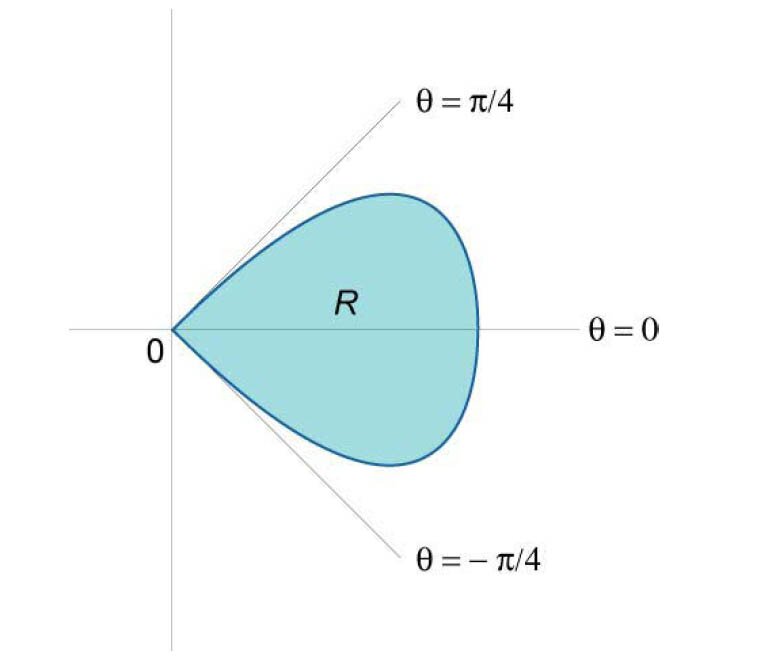
Найти площадь лепестка розы, заданной уравнением \(r = \cos 2\theta.\) Рассмотрим лепесток в секторе \( - \large\frac{\pi }{4}\normalsize \le \theta \le \large\frac{\pi }{4}\normalsize\) (рисунок \(13\)). Область интегрирования имеет вид \(R = \left\{ {\left( {r,\theta } \right)|\;0 \le r \le \cos 2\theta , - \large\frac{\pi }{4}\normalsize \le \theta \le \large\frac{\pi }{4}\normalsize} \right\}.\) Следовательно, площадь данной фигуры в полярных координатах равна \[ {A = \iint\limits_R {rdrd\theta } } = {\int\limits_{ - \large\frac{\pi }{4}\normalsize}^{\large\frac{\pi }{4}\normalsize} {\left[ {\int\limits_0^{\cos 2\theta } {rdr} } \right]d\theta } } = {\int\limits_{ - \large\frac{\pi }{4}\normalsize}^{\large\frac{\pi }{4}\normalsize} {\left[ {\left. {\left( {\frac{{{r^2}}}{2}} \right)} \right|_0^{\cos 2\theta }} \right]d\theta } } = {\frac{1}{2}\int\limits_{ - \large\frac{\pi }{4}\normalsize}^{\large\frac{\pi }{4}\normalsize} {{{\cos }^2}\left( {2\theta } \right)d\theta } } = {\frac{1}{2}\int\limits_{ - \large\frac{\pi }{4}\normalsize}^{\large\frac{\pi }{4}\normalsize} {\frac{{1 + \cos 4\theta }}{2}d\theta } } = {\frac{1}{4}\int\limits_{ - \large\frac{\pi }{4}\normalsize}^{\large\frac{\pi }{4}\normalsize} {\left( {1 + \cos 4\theta } \right)d\theta } } = {\frac{1}{4}\left. {\left( {\theta + \frac{{\sin 4\theta }}{4}} \right)} \right|_{ - \large\frac{\pi }{4}\normalsize}^{\large\frac{\pi }{4}\normalsize} } = {\frac{1}{4}\left[ {\left( {\frac{\pi }{4} + \frac{{\sin \pi }}{4}} \right) - \left( { - \frac{\pi }{4} + \frac{{\sin \left( { - \pi } \right)}}{4}} \right)} \right] } = {\frac{\pi }{8}.} \]

   Пример 8

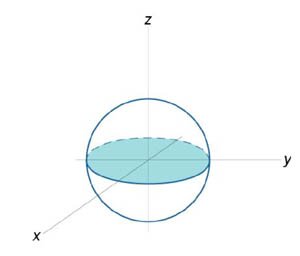
Вычислить объем единичного шара. Уравнение сферы радиусом \(1\) имеет вид \({x^2} + {y^2} + {z^2} = 1\) (рисунок \(14\)). В силу симметрии, ограничимся нахождением объема верхнего полушара и затем результат умножим на \(2.\) Уравнение верхней полусферы записывается как \[z = \sqrt {1 - \left( {{x^2} + {y^2}} \right)} .\] Преобразуя это уравнение в полярные координаты, получаем \[z\left( {r,\theta } \right) = \sqrt {1 - {r^2}} .\] В полярных координатах область интегрирования \(R\) описывается множеством \(R = \left\{ {\left( {r,\theta } \right)|\;0 \le r \le 1,0 \le \theta \le 2\pi } \right\}.\) Следовательно, объем верхнего полушара выражается формулой \[ {{V_{\large\frac{1}{2}\normalsize}} = \iint\limits_R {\sqrt {1 - {r^2}} rdrd\theta } } = {\int\limits_0^{2\pi } {d\theta } \int\limits_0^1 {\sqrt {1 - {r^2}} rdr} } = {2\pi \int\limits_0^1 {\sqrt {1 - {r^2}} rdr} .} \] Сделаем замену переменной для оценки последнего интеграла. Пусть \(1 - {r^2} = t.\) Тогда \(-2rdr = dt\) или \(rdr = - \large\frac{{dt}}{2}\normalsize.\) Уточним пределы интегрирования: \(t = 1\) при \(r = 0\) и, наоборот, \(t = 0\) при \(r = 1.\) Получаем \[ {{V_{\large\frac{1}{2}\normalsize}} = 2\pi \int\limits_0^1 {\sqrt {1 - {r^2}} rdr} } = {2\pi \int\limits_1^0 {\sqrt t \left( { - \frac{{dt}}{2}} \right)} } = { - \pi \int\limits_1^0 {\sqrt t dt} } = {\pi \int\limits_0^1 {{t^{\large\frac{1}{2}\normalsize}}dt} } = {\pi \left. {\left( {\frac{{{t^{\large\frac{3}{2}\normalsize}}}}{{\frac{3}{2}}}} \right)} \right|_0^1 } = {\frac{{2\pi }}{3}.} \] Таким образом, объем единичного шара равен \[V = 2{V_{\large\frac{1}{2}\normalsize}} = \frac{{4\pi }}{3}.\]

   Пример 9

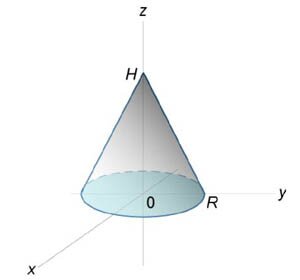
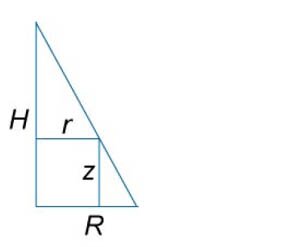
Используя полярные координаты, найти объем конуса высотой \(H\) и радиусом основания \(R\) (рисунок \(15\)). Сначала получим уравнение поверхности конуса. Используя подобные треугольники (рисунок \(16\)), можно записать \[ {\frac{r}{R} = \frac{{H - z}}{H},}\;\; {\text{где}\;\;r = \sqrt {{x^2} + {y^2}} .} \] Следовательно, \[ {H - z = \frac{{Hr}}{R}}\;\; {\text{или}\;\;z\left( {x,y} \right) } = {H - \frac{{Hr}}{R} } = {\frac{H}{R}\left( {R - r} \right) } = {\frac{H}{R}\left( {R - \sqrt {{x^2} + {y^2}} } \right).} \] Тогда объем конуса равен \[ {V = \iint\limits_R {z\left( {x,y} \right)dxdy} } = {\iint\limits_R {\frac{H}{R}\left( {R - \sqrt {{x^2} + {y^2}} } \right)dxdy} } = {\frac{H}{R}\iint\limits_R {\left( {R - r} \right)rdrd\theta } } = {\frac{H}{R}\int\limits_0^{2\pi } {\left[ {\int\limits_0^R {\left( {R - r} \right)drd} } \right]d\theta } } = {\frac{H}{R}\int\limits_0^{2\pi } {d\theta } \int\limits_0^R {\left( {Rr - {r^2}} \right)dr} } = {\frac{{2\pi H}}{R}\int\limits_0^R {\left( {Rr - {r^2}} \right)dr} } = {\frac{{2\pi H}}{R}\left. {\left( {\frac{{R{r^2}}}{2} - \frac{{{r^3}}}{3}} \right)} \right|_{r = 0}^R } = {\frac{{2\pi H}}{R}\left( {\frac{{{R^3}}}{2} - \frac{{{R^3}}}{3}} \right) } = {\frac{{2\pi H}}{R} \cdot \frac{{{R^3}}}{6} = \frac{{\pi {R^2}H}}{3}.} \]

   Пример 10

Вычислить площадь cферы радиуса \(a.\) Рассмотрим верхнюю полусферу. Ее уравнение имеет вид \[ {{x^2} + {y^2} + {z^2} = {a^2}}\;\; {\text{или}\;\;z = \sqrt {{a^2} - {x^2} - {y^2}} .} \] Очевидно, область интегрирования \(R\) представляет собой круг с таким же радиусом \(a,\) расположенный в центре координат. Площадь полусферы вычисляется по формуле \[{S_{\large\frac{1}{2}\normalsize}} = \iint\limits_R {\sqrt {1 + {{\left( {\frac{{\partial z}}{{\partial x}}} \right)}^2} + {{\left( {\frac{{\partial z}}{{\partial y}}} \right)}^2}} dxdy} .\] Найдем частные производные. \[ {\frac{{\partial z}}{{\partial x}} } = {\frac{\partial }{{\partial x}}\sqrt {{a^2} - {x^2} - {y^2}} } = {\frac{{ - \cancel{2}x}}{{\cancel{2}\sqrt {{a^2} - {x^2} - {y^2}} }} } = { - \frac{x}{z},} \] \[ {\frac{{\partial z}}{{\partial y}} } = {\frac{\partial }{{\partial y}}\sqrt {{a^2} - {x^2} - {y^2}} } = {\frac{{ - \cancel{2}y}}{{\cancel{2}\sqrt {{a^2} - {x^2} - {y^2}} }} } = { - \frac{y}{z}.} \] Подставляя найденные производные, получаем \[ {{S_{\large\frac{1}{2}\normalsize}} = \iint\limits_R {\sqrt {1 + {{\left( {\frac{{\partial z}}{{\partial x}}} \right)}^2} + {{\left( {\frac{{\partial z}}{{\partial y}}} \right)}^2}} dxdy} } = {\iint\limits_R {\sqrt {1 + \frac{{{x^2}}}{{{z^2}}} + \frac{{{y^2}}}{{{z^2}}}} dxdy} } = {\iint\limits_R {\sqrt {\frac{{{z^2} + {x^2} + {y^2}}}{{{z^2}}}} dxdy} } = {\iint\limits_R {\frac{a}{z}dxdy} .} \] Преобразуем двойной интеграл в полярные координаты. \[ {{S_{\large\frac{1}{2}\normalsize}} = \iint\limits_R {\frac{a}{z}dxdy} } = {\int\limits_0^{2\pi } {\int\limits_0^a {\frac{a}{{\sqrt {{a^2} - {r^2}} }}rdrd\theta } } } = {a\int\limits_0^{2\pi } {d\theta } \int\limits_0^a {\frac{{rdr}}{{\sqrt {{a^2} - {r^2}} }}} } = { - 2\pi a\int\limits_0^a {\frac{{d\left( {{a^2} - {r^2}} \right)}}{{2\sqrt {{a^2} - {r^2}} }}} } = { - 2\pi a\left. {\left( {\sqrt {{a^2} - {r^2}} } \right)} \right|_{r = 0}^a } = { - 2\pi a\left( {0 - a} \right) = 2\pi {a^2}.} \] Площадь поверхности полной сферы, соответственно, равна \[S = 2{S_{\large\frac{1}{2}\normalsize}} = 4\pi {a^2}.\]