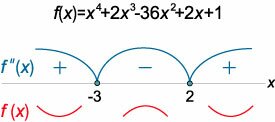Выпуклость функций

Рассмотрим функцию \(y = f\left( x \right),\) которая предполагается непрерывной на отрезке \(\left[ {a,b} \right].\) Функция \(y = f\left( x \right)\) называется выпуклой вниз (или просто выпуклой), если для любых точек \({x_1}\) и \({x_2}\) из \(\left[ {a,b} \right]\) выполняется неравенство \[f\left( {\frac{{{x_1} + {x_2}}}{2}} \right) \le \frac{{f\left( {{x_1}} \right) + f\left( {{x_2}} \right)}}{2}.\] Если данное неравенство является строгим при любых \({x_1},{x_2} \in \left[ {a,b} \right],\) таких, что \({x_1} \ne {x_2},\) то функцию \(f\left( x \right)\) называют строго выпуклой вниз на отрезке \(\left[ {a,b} \right].\)

Аналогично определяется выпуклая вверх функция. Функция \(f\left( x \right)\) называется выпуклой вверх (или вогнутой), если для любых точек \({x_1}\) и \({x_2}\) отрезка \(\left[ {a,b} \right]\) справедливо неравенство \[f\left( {\frac{{{x_1} + {x_2}}}{2}} \right) \ge \frac{{f\left( {{x_1}} \right) + f\left( {{x_2}} \right)}}{2}.\] Если это неравенство является строгим при любых \({x_1},{x_2} \in \left[ {a,b} \right],\) таких, что \({x_1} \ne {x_2},\) то функцию \(f\left( x \right)\) называют строго выпуклой вверх на отрезке \(\left[ {a,b} \right].\) 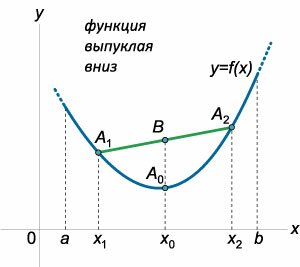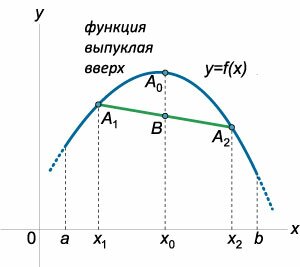Введенные определения выпуклой функции имеют простую геометрическую интерпретацию. Для функции, выпуклой вниз (рисунок \(1\)), середина \(B\) любой хорды \({A_1}{A_2}\) лежит выше соответствующей точки \({A_0}\) графика функции или совпадает с этой точкой.

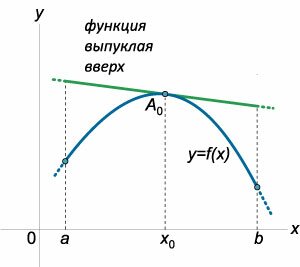
Аналогично, для функции, выпуклой вверх (рисунок \(2\)), середина \(B\) любой хорды \({A_1}{A_2}\) лежит ниже соответствующей точки \({A_0}\) графика функции или совпадает с этой точкой.

Выпуклые функции обладают еще одним наглядным свойством, которое связано с расположением касательной к графику функции. Функция \(f\left( x \right)\) является выпуклой вниз на отрезке \(\left[ {a,b} \right]\) тогда и только тогда, когда ее график лежит не ниже касательной проведенной к нему в любой точке \({x_0}\) отрезка \(\left[ {a,b} \right]\) (рисунок \(3\)). Соответственно, функция \(f\left( x \right)\) является выпуклой вверх на отрезке \(\left[ {a,b} \right]\) тогда и только тогда, когда ее график лежит не выше касательной проведенной к нему в любой точке \({x_0}\) отрезка \(\left[ {a,b} \right]\) (рисунок \(4\)). Данные свойства представляют собой теорему и могут быть доказаны с использованием определения выпуклости функции. Пусть для функции \(f\left( x \right)\) первая производная \(f'\left( x \right)\) существует на отрезке \(\left[ {a,b} \right],\) а вторая производная \(f''\left( x \right)\) − на интервале \(\left( {a,b} \right).\) Тогда справедливы следующие достаточные признаки выпуклости:

• Если \(f''\left( x \right) \ge 0\) при всех \(x \in \left( {a,b} \right),\) то функция \(f\left( x \right)\) выпукла вниз на отрезке \(\left[ {a,b} \right];\)

• Если \(f''\left( x \right) \le 0\) при всех \(x \in \left( {a,b} \right),\) то функция \(f\left( x \right)\) выпукла вверх на отрезке \(\left[ {a,b} \right].\)

В тех случаях, когда вторая производная строго больше (меньше) нуля, говорят, соответственно, о строгой выпуклости вниз (или вверх).

Докажем приведенную теорему для случая выпуклой вниз функции. Пусть функция \(f\left( x \right)\) имеет неотрицательную вторую производную на интервале \(\left( {a,b} \right):\) \(f''\left( x \right) \ge 0.\) Обозначим через \({x_0}\) середину отрезка \(\left[ {{x_1},{x_2}} \right].\) Предположим, что длина этого отрезка равна \(2h.\) Тогда координаты \({x_1}\) и \({x_2}\) можно записать в виде: \[{x_1} = {x_0} - h,\;\;{x_2} = {x_0} + h.\] Разложим функцию \(f\left( x \right)\) в точке \({x_0}\) в ряд Тейлора с остаточным членом в форме Лагранжа. Получаем следующие выражения: \[ {f\left( {{x_1}} \right) = f\left( {{x_0} - h} \right) } = {f\left( {{x_0}} \right) - f'\left( {{x_0}} \right)h + \frac{{f''\left( {{\xi _1}} \right){h^2}}}{{2!}},} \] \[ {f\left( {{x_2}} \right) = f\left( {{x_0} + h} \right) } = {f\left( {{x_0}} \right) + f'\left( {{x_0}} \right)h + \frac{{f''\left( {{\xi _2}} \right){h^2}}}{{2!}},} \] где \({x_0} - h < {\xi _1} < {x_0},\) \({x_0} < {\xi _2} < {x_0} + h.\)

Сложим оба равенства: \[ {f\left( {{x_1}} \right) + f\left( {{x_2}} \right) } = {2f\left( {{x_0}} \right) + \frac{{{h^2}}}{2}\left[ {f''\left( {{\xi _1}} \right) + f''\left( {{\xi _2}} \right)} \right].} \] Поскольку \({\xi _1},{\xi _2} \in \left( {a,b} \right),\) то вторые производные в правой части неотрицательны. Следовательно, \[f\left( {{x_1}} \right) + f\left( {{x_2}} \right) \ge 2f\left( {{x_0}} \right)\] или \[f\left( {\frac{{{x_1} + {x_2}}}{2}} \right) \le \frac{{f\left( {{x_1}} \right) + f\left( {{x_2}} \right)}}{2},\] то есть, в соответствии с определением, функция \(f\left( x \right)\) выпукла вниз.

Отметим, что необходимое условие выпуклости функции (т.е. прямая теорема, в которой, к примеру, из условия выпуклости вниз следует, что \(f''\left( x \right) \ge 0\)) выполняется лишь для нестрогого неравенства. В случае строгой выпуклости необходимое условие, вообще говоря, не соблюдается. Например, функция \(f\left( x \right) = {x^4}\) является строго выпуклой вниз. Однако в точке \(x = 0\) ее вторая производная равна нулю, т.е. строгое неравенство \(f''\left( x \right) \gt 0\) в этом случае не выполняется. Перечислим некоторые свойства выпуклых функций, предполагая, что все функции определены и непрерывны на отрезке \(\left[ {a,b} \right].\)

1. Если функции \(f\) и \(g\) выпуклы вниз (вверх), то любая их линейная комбинация \(af + bg,\) где \(a\), \(b\) − положительные действительные числа, также выпукла вниз (вверх).

2. Если функция \(u = g\left( x \right)\) выпукла вниз, а функция \(y = f\left( u \right)\) является выпуклой вниз и неубывающей, то сложная функция \(y = f\left( {g\left( x \right)} \right)\) будет также выпуклой вниз.

3. Если функция \(u = g\left( x \right)\) выпукла вверх, а функция \(y = f\left( u \right)\) является выпуклой вниз и невозрастающей, то сложная функция \(y = f\left( {g\left( x \right)} \right)\) будет выпуклой вниз.

4. Локальный максимум выпуклой вверх функции, заданной на отрезке \(\left[ {a,b} \right],\) является одновременно ее наибольшим значением на этом отрезке.

5. Локальный минимум выпуклой вниз функции, заданной на отрезке \(\left[ {a,b} \right],\) является одновременно ее наименьшим значением на этом отрезке.

   Пример 1

Изобразить схематически графики функций для всех возможных комбинаций \(y\), \(y'\), \(y''\), в которых каждая из указанных величин является положительной или отрицательной. Рассмотрим произвольную комбинацию данных величин, например следующего вида: \[y > 0,\;\;y' < 0,\;\;y'' > 0.\] График такой функции будет расположен в верхней полуплоскости, а сама функция будет строго убывающей (поскольку \(y' < 0\)). Так как \(y'' > 0,\) то функция выпукла вниз. Ее схематический вид представлен на рисунке \(5\) в первом столбце во втором ряду. Ясно, что полное число возможных комбинаций трех величин с различными знаками равно \(8\). Эскизы соответствующих графиков функций показаны на рисунке \(5\).

   Пример 2

Найти значения \(x\), при которых кубическая функция \(f\left( x \right) = {x^3} + a{x^2} + bx + c\) выпукла вниз. Вычислим вторую производную заданной функции: \[ {f'\left( x \right) = {\left( {{x^3} + a{x^2} + bx + c} \right)^\prime } } = {3{x^2} + 2ax + b;} \] \[ {f''\left( x \right) = {\left( {3{x^2} + 2ax + b} \right)^\prime } } = {6x + 2a.} \] Функция будет выпуклой вверх при условии \(f''\left( x \right) \le 0.\) Находим соответствующие значения \(x:\) \[ {f''\left( x \right) \le 0,}\;\; {\Rightarrow 6x + 2a \le 0,}\;\; {\Rightarrow 6x \le - 2a,}\;\; {\Rightarrow x \le - \frac{a}{3}.} \]

   Пример 3

Найти промежутки выпуклости определенного знака функции \[f\left( x \right) = \sqrt {2 + {x^2}} .\] Данная функция определена и дифференцируема при всех \(x \in \mathbb{R}.\) Вычислим вторую производную: \[\require{cancel} {f'\left( x \right) = {\left( {\sqrt {2 + {x^2}} } \right)^\prime } } = {\frac{1}{{2\sqrt {2 + {x^2}} }} \cdot {\left( {2 + {x^2}} \right)^\prime } } = {\frac{{\cancel{2}x}}{{\cancel{2}\sqrt {2 + {x^2}} }} } = {\frac{x}{{\sqrt {2 + {x^2}} }};} \] \[ {f''\left( x \right) = {\left( {\frac{x}{{\sqrt {2 + {x^2}} }}} \right)^\prime } } = {\frac{{x'\sqrt {2 + {x^2}} - x{{\left( {\sqrt {2 + {x^2}} } \right)}^\prime }}}{{{{\left( {\sqrt {2 + {x^2}} } \right)}^2}}} } = {\frac{{\sqrt {2 + {x^2}} - x \cdot \frac{x}{{\sqrt {2 + {x^2}} }}}}{{2 + {x^2}}} } = {\frac{{{{\left( {\sqrt {2 + {x^2}} } \right)}^2} - {x^2}}}{{\left( {2 + {x^2}} \right)\sqrt {2 + {x^2}} }} } = {\frac{{2 + \cancel{x^2} - \cancel{x^2}}}{{\sqrt {{{\left( {2 + {x^2}} \right)}^3}} }} } = {\frac{2}{{\sqrt {{{\left( {2 + {x^2}} \right)}^3}} }}.} \] Видно, что вторая производная всегда положительна. Поэтому функция выпукла вниз при любых значениях \(x.\)

   Пример 4

Определить характер выпуклости кривой функции \(f\left( x \right) = \arctan x\) в точке \(x = 1.\) Последовательно дифференцируя, находим вторую производную: \[ {f'\left( x \right) = {\left( {\arctan x} \right)^\prime } } = {\frac{1}{{1 + {x^2}}};} \] \[ {f''\left( x \right) = {\left( {\frac{1}{{1 + {x^2}}}} \right)^\prime } } = {{\left[ {{{\left( {1 + {x^2}} \right)}^{ - 1}}} \right]^\prime } } = { - {\left( {1 + {x^2}} \right)^{ - 2}} \cdot 2x } = { - \frac{{2x}}{{{{\left( {1 + {x^2}} \right)}^2}}}.} \] Вычисляем значение второй производной в точке \(x = 1:\) \[ {f''\left( 1 \right) = - \frac{{2 \cdot 1}}{{{{\left( {1 + {1^2}} \right)}^2}}} } = { - \frac{1}{2} < 0.} \] Поскольку вторая производная отрицательна, то функция в этой точке выпукла вниз.

   Пример 5

Найти промежутки выпуклости определенного знака функции \[f\left( x \right) = \frac{1}{{1 + {x^2}}}.\] Функция определена и дифференцируема при всех \(x \in \mathbb{R}.\) Для определения направления выпуклости воспользуемся достаточным признаком и вычислим вторую производную: \[ {f'\left( x \right) = {\left( {\frac{1}{{1 + {x^2}}}} \right)^\prime } } = {{\left[ {{{\left( {1 + {x^2}} \right)}^{ - 1}}} \right]^\prime } } = { - \frac{{2x}}{{{{\left( {1 + {x^2}} \right)}^2}}};} \] \[ {f''\left( x \right) = {\left( { - \frac{{2x}}{{{{\left( {1 + {x^2}} \right)}^2}}}} \right)^\prime } } = { - \frac{{{{\left( {2x} \right)}^\prime }{{\left( {1 + {x^2}} \right)}^2} - 2x{{\left( {{{\left( {1 + {x^2}} \right)}^2}} \right)}^\prime }}}{{{{\left( {1 + {x^2}} \right)}^4}}} } = { - \frac{{2{{\left( {1 + {x^2}} \right)}^2} - 2x \cdot 2\left( {1 + {x^2}} \right) \cdot 2x}}{{{{\left( {1 + {x^2}} \right)}^4}}} } = { - \frac{{2\left( {1 + {x^2}} \right) - 8{x^2}}}{{{{\left( {1 + {x^2}} \right)}^3}}} } = { - \frac{{\color{red}{2} + \color{blue}{2{x^2}} - \color{blue}{8{x^2}}}}{{{{\left( {1 + {x^2}} \right)}^3}}} } = {\frac{{\color{blue}{6{x^2}} - \color{red}{2}}}{{{{\left( {1 + {x^2}} \right)}^3}}}.} \] Найдем интервалы, в которых производная имеет постоянный знак:

1. \( {f''\left( x \right) > 0,}\;\; {\Rightarrow \large\frac{{6{x^2} - 2}}{{{{\left( {1 + {x^2}} \right)}^3}}}\normalsize > 0,}\;\; {\Rightarrow 6{x^2} - 2 > 0,}\;\; {\Rightarrow {x^2} > \large\frac{1}{3}\normalsize,}\;\; {\Rightarrow x \in \left( { - \infty , - \large\frac{1}{{\sqrt 3 }}\normalsize} \right) \cup \left( {\large\frac{1}{{\sqrt 3 }}\normalsize,\infty } \right);} \)

2. \( {f''\left( x \right) < 0,}\;\; {\Rightarrow \large\frac{{6{x^2} - 2}}{{{{\left( {1 + {x^2}} \right)}^3}}}\normalsize < 0,}\;\; {\Rightarrow 6{x^2} - 2 < 0,}\;\; {\Rightarrow {x^2} < \large\frac{1}{3}\normalsize,}\;\; {\Rightarrow x \in \left( { - \large\frac{1}{{\sqrt 3 }}\normalsize,\large\frac{1}{{\sqrt 3 }}\normalsize} \right).} \)

Здесь при решении неравенств мы учли, что знаменатель в выражении для второй производной всегда положителен: \({\left( {1 + {x^2}} \right)^3} > 0.\)

Таким образом, исходя из знака второй производной, устанавливаем, что заданная функция

• строго выпукла вверх в интервале \(\left( { - \large\frac{1}{{\sqrt 3 }}\normalsize,\large\frac{1}{{\sqrt 3 }}\normalsize} \right);\)

• строго выпукла вниз в интервалах \(\left( { - \infty , - \large\frac{1}{{\sqrt 3 }}\normalsize} \right)\) и \(\left( {\large\frac{1}{{\sqrt 3 }}\normalsize, \infty} \right).\)

   Пример 6

Найти промежутки выпуклости вверх и вниз функции \[f\left( x \right) = x - \cos x.\] Последовательно дифференцируя, вычисляем вторую производную: \[ {f'\left( x \right) = {\left( {x - \cos x} \right)^\prime } } = {1 + \sin x,} \] \[ {f''\left( x \right) = {\left( {1 + \sin x} \right)^\prime } } = {\cos x.} \] Определим интервалы, в которых вторая производная положительна и отрицательна. Задача сводится к решению простейшего тригонометрического неравенства: \[ {f''\left( x \right) > 0,}\;\; {\Rightarrow \cos x > 0,}\;\; {\Rightarrow x \in \left( { - \frac{\pi }{2} + 2\pi n,\frac{\pi }{2} + 2\pi n} \right),\;n \in \mathbb{Z};} \] \[ {f''\left( x \right) < 0,}\;\; {\Rightarrow \cos x < 0,}\;\; {\Rightarrow x \in \left( { \frac{\pi }{2} + 2\pi k,\frac{3\pi }{2} + 2\pi k} \right),\;k \in \mathbb{Z}.} \] Следовательно, функция строго выпукла вниз при \(x \in \left( { - \large\frac{\pi }{2}\normalsize + 2\pi n,\large\frac{\pi }{2}\normalsize + 2\pi n} \right),\;n \in \mathbb{Z}\) и строго выпукла вверх при \(x \in \left( { \large\frac{\pi }{2}\normalsize + 2\pi k,\large\frac{3\pi }{2}\normalsize + 2\pi k} \right),\;k \in \mathbb{Z}.\)

Заметим, что линейный член \(x\) в выражении для функции не влияет на характер ее выпуклости.

   Пример 7

Найти промежутки выпуклости вверх и вниз полиномиальной функции \(4\)-го порядка: \[f\left( x \right) = {x^4} + 2{x^3} - 36{x^2} + 2x + 1.\] Последовательно дифференцируя, находим вторую производную: \[ {f'\left( x \right) = {\left( {{x^4} + 2{x^3} - 36{x^2} + 2x + 1} \right)^\prime } } = {4{x^3} + 6{x^2} - 72x + 2;} \] \[ {f''\left( x \right) = {\left( {4{x^3} + 6{x^2} - 72x + 2} \right)^\prime } } = {12{x^2} + 12x - 72 } = {12\left( {{x^2} + x - 6} \right).} \] Решим уравнение \(f''\left( x \right) = 0\) и определим знаки второй производной в соответствующих интервалах (рисунок \(6\)): \[ {f''\left( x \right) = 0,}\;\; {\Rightarrow 12\left( {{x^2} + x - 6} \right) = 0,}\;\; {\Rightarrow D = 1 + 4 \cdot \left( { - 6} \right) = 25,}\;\; {\Rightarrow {x_{1,2}} = \frac{{ - 1 \pm 5}}{2} = - 3;2.} \] Следовательно, данная функция (а также ее кривая) строго выпукла вниз в интервалах \(\left( { - \infty , - 3} \right)\) и \(\left( {2, + \infty } \right)\) и строго выпукла вверх в интервале \(\left( {-3, 2} \right).\)

   Пример 8

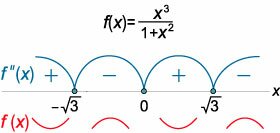
Найти промежутки выпуклости определенного знака функции \[f\left( x \right) = \frac{{{x^3}}}{{1 + {x^2}}}.\] Очевидно, данная функция определена и дифференцируема при любых \(x.\) Находим последовательно первую и вторую производные: \[ {f'\left( x \right) = {\left( {\frac{{{x^3}}}{{1 + {x^2}}}} \right)^\prime } } = {\frac{{{{\left( {{x^3}} \right)}^\prime }\left( {1 + {x^2}} \right) - {x^3}{{\left( {1 + {x^2}} \right)}^\prime }}}{{{{\left( {1 + {x^2}} \right)}^2}}} } = {\frac{{3{x^2}\left( {1 + {x^2}} \right) - {x^3} \cdot 2x}}{{{{\left( {1 + {x^2}} \right)}^2}}} } = {\frac{{\color{blue}{3{x^2}} + \color{red}{3{x^4}} - \color{red}{2{x^4}}}}{{{{\left( {1 + {x^2}} \right)}^2}}} } = {\frac{{\color{blue}{3{x^2}} + \color{red}{x^4}}}{{{{\left( {1 + {x^2}} \right)}^2}}};} \] \[ {f''\left( x \right) = {\left( {\frac{{3{x^2} + {x^4}}}{{{{\left( {1 + {x^2}} \right)}^2}}}} \right)^\prime } } = {\frac{{{{\left( {3{x^2} + {x^4}} \right)}^\prime }{{\left( {1 + {x^2}} \right)}^2} - \left( {3{x^2} + {x^4}} \right){{\left( {{{\left( {1 + {x^2}} \right)}^2}} \right)}^\prime }}}{{{{\left( {1 + {x^2}} \right)}^4}}} } = {\frac{{\left( {6x + 4{x^3}} \right){{\left( {1 + {x^2}} \right)}^2} - \left( {3{x^2} + {x^4}} \right) \cdot 2\left( {1 + {x^2}} \right) \cdot 2x}}{{{{\left( {1 + {x^2}} \right)}^4}}} } = {\frac{{\left( {6x + 4{x^3}} \right)\left( {1 + {x^2}} \right) - 4x\left( {3{x^2} + {x^4}} \right)}}{{{{\left( {1 + {x^2}} \right)}^3}}} } = {\frac{{\color{green}{6x} + \color{maroon}{4{x^3}} + \color{maroon}{6{x^3}} + \cancel{\color{maroon}{4{x^3}}} - \color{maroon}{12{x^3}} - \cancel{\color{maroon}{4{x^3}}}}}{{{{\left( {1 + {x^2}} \right)}^3}}} } = {\frac{{\color{green}{6x} - \color{maroon}{2{x^3}}}}{{{{\left( {1 + {x^2}} \right)}^3}}}.} \] Определим интервалы знакопостоянства второй производной. Она имеет нули в следующих точках: \[ {f''\left( x \right) = 0,}\;\; {\Rightarrow \frac{{6x - 2{x^3}}}{{{{\left( {1 + {x^2}} \right)}^3}}} = 0,}\;\; {\Rightarrow \left\{ {\begin{array}{*{20}{l}} {6x - 2{x^3} = 0}\\ {{{\left( {1 + {x^2}} \right)}^3} \ne 0} \end{array}} \right.,}\;\; {\Rightarrow 2x\left( {3 - {x^2}} \right) = 0,}\;\; {\Rightarrow {x_1} = 0,\;{x_{2,3}} = \pm \sqrt 3 .} \] Из рисунка \(6\) (приведенного выше) видно, что вторая производная положительна в интервалах \(\left( { - \infty , - \sqrt 3 } \right)\) и \(\left( {0, \sqrt 3 } \right).\) Следовательно, здесь функция является строго выпуклой вниз. В двух других интервалах − при \(x \in \left( {-\sqrt 3, 0} \right)\) и при \(x \in \left( {\sqrt 3, +\infty} \right)\) − функция строго выпукла вверх, как схематически показано на рисунке \(7.\)

   Пример 9

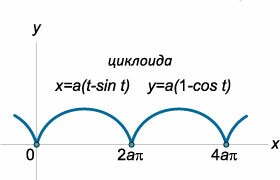
Исследовать направление выпуклости кривой, заданной параметрическими уравнениями \[ {x = a\left( {t - \sin t} \right),}\;\; {y = a\left( {1 - \cos t} \right),} \] где \(a > 0.\) Данная кривая представляет собой циклоиду. Вычислим сначала производную первого порядка: \[ {{x'_t} = {\left[ {a\left( {t - \sin t} \right)} \right]^\prime } = a\left( {1 - \cos t} \right),}\;\; {{y'_t} = {\left[ {a\left( {1 - \cos t} \right)} \right]^\prime } = a\sin t,}\;\; {\Rightarrow {y'_x} = \frac{{{y'_t}}}{{{x'_t}}} } = {\frac{{\cancel{a}\sin t}}{{\cancel{a}\left( {1 - \cos t} \right)}} } = {\frac{{\sin t}}{{1 - \cos t}}.} \] Производная второго порядка определяется по формуле: \[{y''_{xx}} = \frac{{{{\left( {{y'_x}} \right)}'_t}}}{{{x'_t}}},\] где \[ {{\left( {{y'_x}} \right)'_t} = {\left( {\frac{{\sin t}}{{1 - \cos t}}} \right)^\prime } } = {\frac{{{{\left( {\sin t} \right)}^\prime }\left( {1 - \cos t} \right) - \sin t{{\left( {1 - \cos t} \right)}^\prime }}}{{{{\left( {1 - \cos t} \right)}^2}}} } = {\frac{{\cos t\left( {1 - \cos t} \right) - \sin t\sin t}}{{{{\left( {1 - \cos t} \right)}^2}}} } = {\frac{{\cos t - \left( {{{\cos }^2}t + {{\sin }^2}t} \right)}}{{{{\left( {1 - \cos t} \right)}^2}}} } = { - \frac{\cancel{1 - \cos t}}{{{{\left( {1 - \cos t} \right)}^\cancel{2}}}} } = { - \frac{1}{{1 - \cos t}}.} \] Следовательно, вторая производная имеет вид: \[ {{y''_{xx}} = \frac{{{{\left( {{y'_x}} \right)}'_t}}}{{{x'_t}}} } = {\frac{{\left( { - \frac{1}{{1 - \cos t}}} \right)}}{{1 - \cos t}} } = { - \frac{1}{{{{\left( {1 - \cos t} \right)}^2}}}.} \] Как видно, производная \(y''\) всюду отрицательна, кроме точек \(t = 2\pi n,\;n \in \mathbb{Z}.\) Для данных точек \(x\)-координата равна \[ {x\left( {t = 2\pi n} \right) } = {a\left[ {2\pi n - \sin \left( {2\pi n} \right)} \right] } = {2a\pi n,\;n \in \mathbb{Z}.} \] Участок циклоиды схематически показан на рисунке \(8\).

   Пример 10

Исследовать направление выпуклости кривой, заданной неявным уравнением \[x + y = {e^{x - y}}.\] Дифференцируя левую и правую части уравнения по \(x,\) находим первую производную: \[ {{\left( {x + y} \right)^\prime } = {\left( {{e^{x - y}}} \right)^\prime },}\;\; {\Rightarrow 1 + y' = {e^{x - y}}\left( {1 - y'} \right),}\;\; {\Rightarrow 1 + y' = {e^{x - y}} - {e^{x - y}}y',}\;\; {\Rightarrow y'\left( {{e^{x - y}} + 1} \right) = {e^{x - y}} - 1,}\;\; {\Rightarrow y' = \frac{{{e^{x - y}} - 1}}{{{e^{x - y}} + 1}}.} \] Аналогично определяем вторую производную: \[ {y'\left( {{e^{x - y}} + 1} \right) = {e^{x - y}} - 1,}\;\; {\Rightarrow {\left( {y'\left( {{e^{x - y}} + 1} \right)} \right)^\prime } = {\left( {{e^{x - y}} - 1} \right)^\prime },}\;\; {\Rightarrow y''\left( {{e^{x - y}} + 1} \right) + y'{e^{x - y}}\left( {1 - y'} \right) = {e^{x - y}}\left( {1 - y'} \right),}\;\; {\Rightarrow y''\left( {{e^{x - y}} + 1} \right) = {e^{x - y}}\left( {1 - y'} \right) - {e^{x - y}}\left( {1 - y'} \right)y',}\;\; {\Rightarrow y''\left( {{e^{x - y}} + 1} \right) = {e^{x - y}}{\left( {1 - y'} \right)^2},}\;\; {\Rightarrow y'' = \frac{{{e^{x - y}}{{\left( {1 - y'} \right)}^2}}}{{{e^{x - y}} + 1}}.} \] Подставим в последнее выражение первую производную \(y':\) \[ y'' = \frac{{{e^{x - y}}{{\left( {1 - y'} \right)}^2}}}{{{e^{x - y}} + 1}} = \frac{{{e^{x - y}}{{\left( {1 - \frac{{{e^{x - y}} - 1}}{{{e^{x - y}} + 1}}} \right)}^2}}}{{{e^{x - y}} + 1}} = \frac{{{e^{x - y}}{{\left( {\frac{{\cancel{e^{x - y}} + 1 - \cancel{e^{x - y}} + 1}}{{{e^{x - y}} + 1}}} \right)}^2}}}{{{e^{x - y}} + 1}} = \frac{{4{e^{x - y}}}}{{{{\left( {{e^{x - y}} + 1} \right)}^3}}}. \] Поскольку экспоненциальная функция всегда положительна, то вторая производная также положительна при всех \(x \in \mathbb{R}.\) Следовательно, заданная кривая всюду строго выпукла вниз.