Барометрическая формула

В данном разделе мы выведем зависимость давления газа \(P\) от высоты \(h\) над уровнем моря в гравитационном поле Земли.

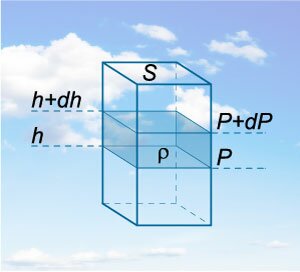
Возьмем произвольную цилиндрическую колонну газа с площадью сечения \(S\) и высотой \(h.\) Вес выделенного объема газа будет равен \[F = mg = \rho gV = \rho ghS,\] где \(\rho\) означает плотность газа. Плотность газа будет выражаться следующей формулой: \[\require{cancel} P = \frac{F}{S} = \frac{{\rho gh\cancel{S}}}{\cancel{S}} = \rho gh. \] Теперь представим такую колонну в атмосфере и выделим в ней тонкий слой воздуха высотой \(dh\) (рисунок \(1\)). Ясно, что такой слой вызывает изменение давления на величину \[dP = - \rho gdh.\] Мы поставили здесь знак минус, поскольку давление должно уменьшаться с увеличением высоты. Рассматривая атмосферный воздух как идеальный газ, воспользуемся уравнением Менделеева-Клапейрона, чтобы выразить плотность \(\rho\) через давление \(P:\) \[ {PV = \frac{m}{M}RT,}\;\; {\Rightarrow P = \frac{m}{{VM}}RT = \frac{\rho }{M}RT.} \] Здесь \(T\) − абсолютная температура, \(R\) − универсальная газовая постояная, равная \(8.314\,{\large\frac{\text{Дж}}{K \cdot \text{моль}}\normalsize},\) \(M\) − молярная масса, которая для воздуха равна \(0.029\,{\large\frac{\text{кг}}{\text{моль}}\normalsize}.\) Отсюда следует, что плотность определяется формулой \[\rho = \frac{{MP}}{{RT}}.\] Подставляя это в дифференциальное соотношение для \(dP,\) находим: \[ {dP = - \rho gdh = - \frac{{MP}}{{RT}}gdh,}\;\; {\Rightarrow \frac{{dP}}{P} = - \frac{{Mg}}{{RT}}dh.} \] В результате мы получаем дифференциальное уравнение, описывающее давление газа \(P\) как функцию высоты \(h.\) Интегрирование приводит к следующему уравнению: \[ {\int {\frac{{dP}}{P}} = - \int {\frac{{Mg}}{{RT}}dh} ,}\;\; {\Rightarrow \ln P = - \frac{{Mg}}{{RT}}h + \ln C.} \] Избавляясь от логарифмов, получаем так называемую барометрическую формулу \[P = C\exp \left( { - \frac{{Mg}}{{RT}}h} \right).\] Константа \(C\) определяется из начального условия \(P\left( {h = 0} \right) = {P_0},\) где \({P_0}\) − это среднее атмосферное давление над уровнем моря.

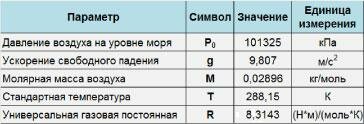
Таким образом, зависимость атмосферного давления от высоты выражается формулой: \[P = {P_0}\exp \left( { - \frac{{Mg}}{{RT}}h} \right).\] Подставляя известные стандартные значения (смотрите рисунок \(2\) выше), находим зависимость \(P\left( h \right)\) (в килопаскалях), которая описывается формулой \[ {P\left( h \right) = 101.325\exp \left( { - \frac{{0.02896 \cdot 9.807}}{{8.3143 \cdot 288.15}}h} \right) } = {101.325\exp \left( { - 0.00012\,h} \right)\;\left[\text{кПа} \right],} \] где высота \(h\) над уровнем моря выражается в метрах.

Если давление определяется в миллиметрах ртутного столба \(\left( \text{мм.рт.ст.} \right),\) то барометрическая формула принимает вид: \[P\left( h \right) = 760\exp \left( { - 0.00012\,h} \right)\;\left[ \text{мм.рт.ст.} \right].\] Барометрическая формула широко используется для оценки атмосферного давления при различных условиях, хотя она дает слегка завышенные значения.

   Пример 1

Определить на какой высоте давление воздуха в два раза ниже, чем на уровне моря? Для оценки высоты воспользуемся барометрической формулой: \[P\left( h \right) = {P_0}\exp \left( { - 0.00012\,h} \right).\] При \(h = 0\) давление \(P\left( h \right)\) равно среднему атмосферному давлению на уровне моря \({P_0}.\) На некоторой высоте \(H\) давление будет в два раза меньше: \[P\left( H \right) = \frac{{{P_0}}}{2} = {P_0}\exp \left( { - 0.00012\,H} \right).\] Отсюда следует, что \[\exp \left( { - 0.00012\,H} \right) = \frac{1}{2}.\] Взяв логарифм от обеих частей, найдем высоту \(H:\) \[ {\ln \frac{1}{2} = - 0.00012\,H,}\;\; {\Rightarrow \ln 2 = 0.00012\,H,}\;\; {\Rightarrow H = \frac{{\ln 2}}{{0.00012}} \approx 5780\,\text{м}.} \]

   Пример 2

Найти давление воздуха в шахте на глубине \(1\,\text{км}\) при температуре \(40\) градусов Цельсия. Давление воздуха в шахте можно оценить, используя общую барометрическую формулу: \[P = {P_0}\exp \left( { - \frac{{Mg}}{{RT}}h} \right).\] Подставим в эту формулу следующие значения: \(h = - 1000\,\text{м}\) (знак минус соответствует расположению ниже уровня моря), \(T = 40 + 273.15 = 313.15\,\text{К}.\) Остальные параметры являются стандартными: \(M = 0.02896\,\large\frac{\text{кг}}{\text{моль}}\normalsize,\) \(R = 8.3143\,\large\frac{\text{Н}\cdot\text{м}}{\text{моль}\cdot\text{К}}\normalsize,\) \(g = 9.807\,\large\frac{\text{м}}{\text{с}^2}\normalsize.\)

После несложных вычислений находим: \[ {P = {P_0}\exp \left( { - \frac{{Mg}}{{RT}}h} \right) } = {{P_0}\exp \left[ { - \frac{{0.02896 \cdot 9.807}}{{8.3143 \cdot 313.15}}\left( { - 1000} \right)} \right] } \approx {{P_0}\exp \left( {0.109} \right) } \approx {1.115{P_0}.} \] Поскольку атмосферное давление на уровне моря составляет \({P_0} = 760\;\text{мм.рт.ст.},\) то давление воздуха в шахте будет равно \(848\;\text{мм.рт.ст.},\) что примерно на \(12\%\) выше стандартного давления на уровне моря.