|
Асимптоты
|
||||||||||||
|
Асимптотой кривой \(y = f\left( x \right),\) имеющей бесконечную ветвь, называется прямая, расстояние которой от точки \(\left( {x,f\left( x \right)} \right),\) лежащей на кривой, стремится к нулю при неограниченном движении вдоль ветви к бесконечности.
Асимптоты могут быть вертикальными, наклонными и горизонтальными. Горизонтальную асимптоту часто рассматривают как частный случай наклонной асимптоты.
Вертикальная асимптота
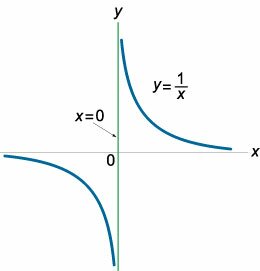
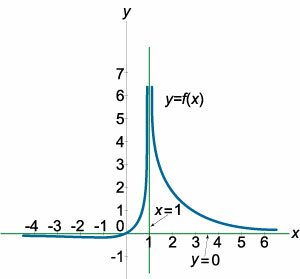
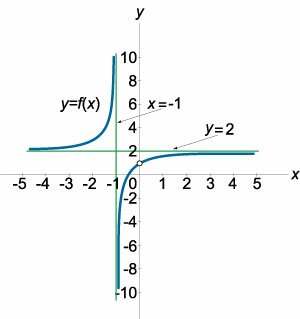
Прямая \(x = a\) является вертикальной асимптотой графика функции \(y = f\left( x \right),\) если выполнено хотя бы одно из условий: \[\lim\limits_{x \to a - 0} f\left( x \right) = \pm \infty ,\;\;\;\lim\limits_{x \to a + 0} f\left( x \right) = \pm \infty .\] Другими словами, хотя бы один из односторонних пределов в точке \(x = a\) должен быть равен бесконечности.Вертикальная асимптота часто встречается у дробно-рациональных функций в точках, где знаменатель равен нулю, а числитель не равен нулю (т.е. в точках разрыва второго рода). Например, график функции \(y = \large\frac{1}{x}\normalsize\) имеет вертикальную асимптоту \(x = 0\) (рисунок 1). В данном случае оба односторонних предела (слева и справа) стремятся к бесконечности: \[\lim\limits_{x \to 0 - 0} \frac{1}{x} = - \infty ,\;\;\;\lim\limits_{x \to 0 + 0} \frac{1}{x} = + \infty .\] Функции, которые являются непрерывными на всем множестве действительных чисел, вертикальных асимптот не имеют.
Наклонная асимптота
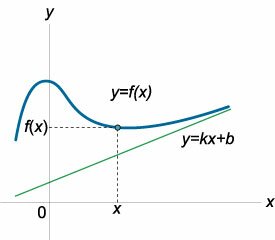
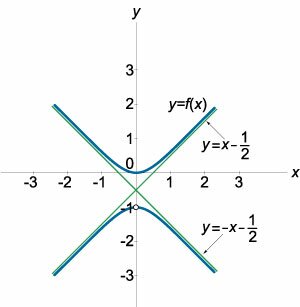
Прямая \(y = kx + b\) называется наклонной асимптотой графика функции \(y = f\left( x \right),\) при \(x \to +\infty\) (рисунок \(2\)), если \[\lim\limits_{x \to + \infty } \left[ {f\left( x \right) - \left( {kx + b} \right)} \right] = 0.\] Аналогично вводится понятие наклонной асимптоты при \(x \to -\infty.\)Наклонные асимптоты графика функции \(y = f\left( x \right)\) могут быть разными при \(x \to +\infty\) и \(x \to -\infty.\) Поэтому при нахождении наклонных (или горизонтальных) асимптот оба случая следует рассматривать отдельно. Коэффициенты \(k\) и \(b\) наклонной асимптоты \(y = kx + b\) определяются с помощью следующей теоремы: Для того, чтобы прямая \(y = kx + b\) была асимптотой графика функции \(y = f\left( x \right)\) при \(x \to +\infty,\) необходимо и достаточно, чтобы существовали два конечных предела: \[ {\lim\limits_{x \to + \infty } \frac{{f\left( x \right)}}{x} = k}\;\;\; {\text{и}\;\;\lim\limits_{x \to + \infty } \left[ {f\left( x \right) - kx} \right] = b.} \] Доказательство. Необходимость. Пусть прямая \(y = kx + b\) является асимптотой графика функции \(y = f\left( x \right)\) при \(x \to +\infty.\) Тогда выполняется условие \[\lim\limits_{x \to + \infty } \left[ {f\left( x \right) - \left( {kx + b} \right)} \right] = 0\] или равносильное соотношение \[ {f\left( x \right) = kx + b + \alpha \left( x \right),}\;\;\; {\text{где}\;\;\lim\limits_{x \to + \infty } \alpha \left( x \right) = 0.} \] Разделив обе части последнего равенства на \(x,\) получаем: \[ {\frac{{f\left( x \right)}}{x} = \frac{{kx + b + \alpha \left( x \right)}}{x},}\;\; {\Rightarrow \frac{{f\left( x \right)}}{x} = k + \frac{b}{x} + \frac{{\alpha \left( x \right)}}{x}.} \] Следовательно, в пределе при \(x \to +\infty\) имеем: \[ {\lim\limits_{x \to + \infty } \frac{{f\left( x \right)}}{x} } = {\lim\limits_{x \to + \infty } \left[ {k + \frac{b}{x} + \frac{{\alpha \left( x \right)}}{x}} \right] = k,} \] \[ {\lim\limits_{x \to + \infty } \left[ {f\left( x \right) - kx} \right] } = {\lim\limits_{x \to + \infty } \left[ {b + \alpha \left( x \right)} \right] = b.} \] Достаточность. Пусть существуют конечные пределы: \[ {\lim\limits_{x \to + \infty } \frac{{f\left( x \right)}}{x} = k\;\;\;\text{и}}\;\; {\lim\limits_{x \to + \infty } \left[ {f\left( x \right) - kx} \right] = b.} \] Второй предел можно записать в виде \[\lim\limits_{x \to + \infty } \left[ {f\left( x \right) - \left( {kx + b} \right)} \right] = 0,\] что соответствует определению наклонной асимптоты. Таким образом, прямая \(y = kx + b\) асимптота графика функции \(y = f\left( x \right).\) Замечание: Аналогично доказывается теорема для случая \(x \to -\infty.\)
Горизонтальная асимптота
В частном случае, если \(k = 0,\) мы получаем горизонтальную асимптоту, которая описывается уравнением \(y = b.\) Теорема о необходимых и достаточных условиях существования горизонтальной асимптоты формулируется таким образом:Для того, чтобы прямая \(y = b\) была асимптотой графика функции \(y = f\left( x \right)\) при \(x \to +\infty,\) необходимо и достаточно, чтобы существовал конечный предел: \[\lim\limits_{x \to + \infty } f\left( x \right) = b.\] Точно также рассматривается случай \(x \to -\infty.\)
Асимптоты кривой, заданной параметрически
Пусть плоская кривая задана параметрическими уравнениями \[x = \varphi \left( t \right),\;\;\;y = \psi \left( t \right).\] Данная линия имеет вертикальную асимптоту \(x = a\) при \(t \to {t_1},\) если выполняются условия \[ \lim\limits_{t \to {t_1}} \varphi \left( t \right) = a\;\;\;\text{и}\;\;\; \lim\limits_{t \to {t_1}} \psi \left( t \right) = \pm \infty . \] Аналогично, параметрически заданная линия имеет горизонтальную асимптоту \(y = b\) при \(t \to {t_2},\) если выполняются следующие соотношения: \[ \lim\limits_{t \to {t_2}} \varphi \left( t \right) = \pm \infty\;\;\;\text{и}\;\;\; \lim\limits_{t \to {t_2}} \psi \left( t \right) = b. \] Здесь \(a\) и \(b\) являются конечными величинами.Параметрически заданная кривая имеет наклонную асимптоту \(y = kx + b\) при \(t \to {t_3},\) если при этом значении \(t\) оба предела равны бесконечности: \[ {\lim\limits_{t \to {t_3}} \varphi \left( t \right) = \pm \infty ,}\;\;\; {\lim\limits_{t \to {t_3}} \psi \left( t \right) = \pm \infty ,} \] а коэффициенты \(k\) и \(b\) имеют конечные значения: \[ {k = \lim\limits_{t \to {t_3}} \frac{{\psi \left( t \right)}}{{\varphi \left( t \right)}},}\;\;\; {b = \lim\limits_{t \to {t_3}} \left[ {\psi \left( t \right) - k\varphi \left( t \right)} \right].} \]
Асимптота кривой в полярных координатах
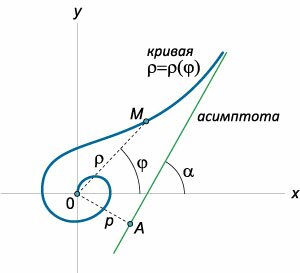
Рассмотрим кривую, заданную в полярных координатах уравнением \[\rho = \rho \left( \varphi \right)\;\;\;\text{или}\;\;F\left( {\rho ,\varphi } \right) = 0.\] Ее асимптоту (если она существует) можно описать с помощью двух параметров − расстояния \(p\) от центра до асимптоты (отрезок \(OA\) на рисунке \(3\)) и угла \(\alpha\) наклона асимптоты к полярной оси.Указанные параметры \(\alpha\) и \(p\) определяются формулами: \[ {\alpha = \lim\limits_{\rho \to \infty } \varphi ,}\;\;\; {p = \lim\limits_{\rho \to \infty } \left[ {\rho \sin \left( {\alpha - \varphi } \right)} \right].} \] Замечания:
Асимптоты кривой, заданной неявно
Неявно заданная алгебраическая кривая описывается уравнением \[F\left( {x,y} \right) = 0,\] где левая часть представляет собой многочлен относительно переменных \(x\) и \(y.\)В дифференциальной геометрии используется следующий метод нахождения наклонной асимптоты алгебраической кривой. Пусть асимптота описывается уравнением \(y = kx + b.\) Подставляя это выражение для \(y\) в уравнение кривой, получаем алгебраическое уравнение относительно одной переменной \(x:\) \[{A_0}{x^n} + {A_1}{x^{n - 1}} + \ldots + {A_{n - 1}}x + {A_n} = 0,\] где коэффициенты \({A_i}\) зависят от параметров асимптоты \(k\) и \(b\) (причем коэффициент \({A_0}\) зависит лишь от \(k\)). Значения \(k\) и \(b\) определяются из условия: \[\left\{ \begin{array}{l} {A_0}\left( k \right) = 0\\ {A_1}\left( {k,b} \right) = 0 \end{array} \right..\] Для нахождения вертикальной асимптоты нужно подставить ее уравнение \(x = a\) в уравнение кривой и преобразовать последнее к виду: \[{B_0}{y^n} + {B_1}{y^{n - 1}} + \ldots + {B_{n - 1}}y + {B_n} = 0.\] Необходимым условием существования вертикальной асимптоты является отсутствие в последнем уравнении старшего члена \({B_0}{y^n}.\) Значение параметра \(a\) определяется из условия \[{B_1}\left( a \right) = 0.\] Приведенные формулы для асимптот неявно заданных кривых справедливы, если кривая не имеет особых точек на бесконечности. |
||||||||||||
|
Пример 1
|
||||||||||||
|
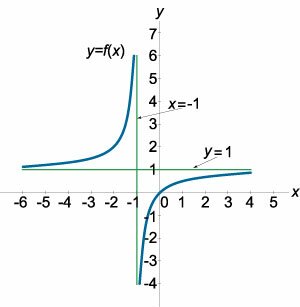
Найти асимптоты графика функции \[y = \frac{x}{{x + 1}}.\]
Решение.
При \(x = -1\) функция имеет разрыв второго рода. Действительно: \[ {\lim\limits_{x \to - 1 - 0} f\left( x \right) } = {\lim\limits_{x \to - 1 - 0} \frac{x}{{x + 1}} } = {\frac{{ - 1}}{{\left( { - 1 - 0} \right) + 1}} } = {\frac{{ - 1}}{{ - 0}} = + \infty ,} \] \[ {\lim\limits_{x \to - 1 + 0} f\left( x \right) } = {\lim\limits_{x \to - 1 + 0} \frac{x}{{x + 1}} } = {\frac{{ - 1}}{{\left( { - 1 + 0} \right) + 1}} } = {\frac{{ - 1}}{{ + 0}} = - \infty .} \] Следовательно, \(x = -1\) − уравнение вертикальной асимптоты.Найдем горизонтальную асимптоту. Вычислим предел: \[\lim\limits_{x \to \pm \infty } \frac{x}{{x + 1}} = \lim\limits_{x \to \pm \infty } \frac{1}{{1 + \frac{1}{x}}} = 1.\] Таким образом у кривой существует горизонтальная асимптота, и ее уравнение имеет вид \(y = 1.\) Наклонные асимптоты отсутствуют. Это можно проверить, вычислив коэффициенты \(k\) и \(b:\) \[ {k = \lim\limits_{x \to \pm \infty } \frac{{y\left( x \right)}}{x} } = {\lim\limits_{x \to \pm \infty } \frac{x}{{\left( {x + 1} \right)x}} } = {\lim\limits_{x \to \pm \infty } \frac{x}{{{x^2} + x}} } = {\lim\limits_{x \to \pm \infty } \frac{{\frac{1}{x}}}{{1 + \frac{1}{x}}} = 0,} \] \[ {b = \lim\limits_{x \to \pm \infty } \left[ {y\left( x \right) - kx} \right] } = {\lim\limits_{x \to \pm \infty } \left( {\frac{x}{{x + 1}} - 0} \right) } = {\lim\limits_{x \to \pm \infty } \frac{1}{{1 + \frac{1}{x}}} = 1.} \] Видно, что на самом деле мы получили горизонтальную асимптоту, которая уже была определена выше. Окончательный ответ: график функции имеет вертикальную асимптоту \(x = -1\) и горизонтальную асимптоту \(y = 1\) (рисунок \(4\)). |
||||||||||||
|
Пример 2
|
||||||||||||
|
Найти асимптоты графика функции \[y = \frac{x}{{{{\left( {x - 1} \right)}^2}}}.\]
Решение.
Вычислим односторонние пределы в точке \(x = 1:\) \[ {\lim\limits_{x \to 1 - 0} y\left( x \right) } = {\lim\limits_{x \to 1 - 0} \frac{x}{{{{\left( {x - 1} \right)}^2}}} } = {\frac{{1 - 0}}{{{{\left( {1 - 0 - 1} \right)}^2}}} } = {\frac{1}{{{{\left( { - 0} \right)}^2}}} = + \infty ,} \] \[ {\lim\limits_{x \to 1 + 0} y\left( x \right) } = {\lim\limits_{x \to 1 + 0} \frac{x}{{{{\left( {x - 1} \right)}^2}}} } = {\frac{{1 + 0}}{{{{\left( {1 + 0 - 1} \right)}^2}}} } = {\frac{1}{{{{\left( { + 0} \right)}^2}}} = + \infty.} \] Пределы равны бесконечности. Следовательно, \(x = 1\) является вертикальной асимптотой для заданной кривой.Исследуем наклонные асимптоты: \[\require{cancel} {k = \lim\limits_{x \to \pm \infty } \frac{{y\left( x \right)}}{x} } = {\lim\limits_{x \to \pm \infty } \frac{\cancel{x}}{{{{\left( {x - 1} \right)}^2}\cancel{x}}} } = {\lim\limits_{x \to \pm \infty } \frac{1}{{{{\left( {x - 1} \right)}^2}}} = 0;} \] \[ {b = \lim\limits_{x \to \pm \infty } \left[ {y\left( x \right) - kx} \right] } = {\lim\limits_{x \to \pm \infty } \left[ {\frac{x}{{{{\left( {x - 1} \right)}^2}}} - 0} \right] } = {\lim\limits_{x \to \pm \infty } \frac{x}{{{x^2} - 2x + 1}} } = {\lim\limits_{x \to \pm \infty } \frac{{\frac{1}{x}}}{{1 - \frac{2}{x} + \frac{1}{{{x^2}}}}} = 0.} \] Отсюда видно, что существует не наклонная, а горизонтальная асимптота при \(x \to \pm \infty.\) Ее уравнение имеет вид \(y = 0,\) т.е. асимптотой является ось абсцисс. График функции и его асимптоты приведены на рисунке \(5.\)
|
||||||||||||
|
Пример 3
|
||||||||||||
|
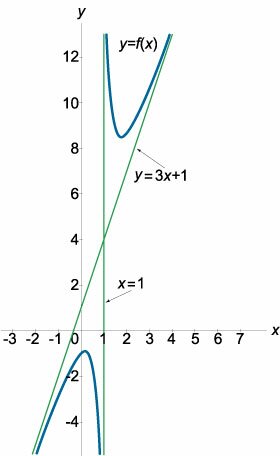
Найти асимптоты графика функции \[y = \frac{{3{x^2} - 2x + 1}}{{x - 1}}.\]
Решение.
Ясно, что прямая \(x = 1\) является вертикальной асимптотой, поскольку в этой точке функция имеет разрыв и выполняются соотношения \[ {\lim\limits_{x \to 1 - 0} y\left( x \right) } = {\lim\limits_{x \to 1 - 0} \frac{{3{x^2} - 2x + 1}}{{x - 1}} } = {\frac{{3{{\left( {1 - 0} \right)}^2} - 2\left( {1 - 0} \right) + 1}}{{1 - 0 - 1}} = - \infty ,} \] \[ {\lim\limits_{x \to 1 + 0} y\left( x \right) } = {\lim\limits_{x \to 1 + 0} \frac{{3{x^2} - 2x + 1}}{{x - 1}} } = {\frac{{3{{\left( {1 + 0} \right)}^2} - 2\left( {1 + 0} \right) + 1}}{{1 + 0 - 1}} = + \infty .} \] Запишем функцию в виде \[ {y = \frac{{3{x^2} - 2x + 1}}{{x - 1}} } = {\frac{{3{x^2} - 3x + x - 1 + 2}}{{x - 1}} } = {\frac{{3x\cancel{\left( {x - 1} \right)}}}{\cancel{x - 1}} + \frac{\cancel{x - 1}}{\cancel{x - 1}} + \frac{2}{{x - 1}} } = {3x + 1 + \frac{2}{{x - 1}} = 3x + 1 + \alpha \left( x \right),} \] где \(\alpha \left( x \right) \to 0\) при \(x \to \pm \infty.\)Таким образом, график функции имеет наклонную асимптоту \(y = 3x + 1.\) Заметим, что дробно-рациональная функция может иметь наклонную асимптоту, если степень числителя на единицу больше степени знаменателя. Схематический вид данной кривой приведен выше на рисунке \(6.\) |
||||||||||||
|
Пример 4
|
||||||||||||
|
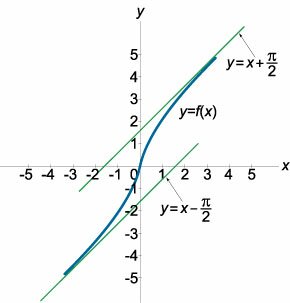
Найти асимптоты графика функции \[y = x + \arctan x.\]
Решение.
Данная функция непрерывна на всем множестве действительных чисел. Поэтому у нее нет вертикальных асимптот. Исследуем наклонные асимптоты: \[ {k = \lim\limits_{x \to \pm \infty } \frac{{y\left( x \right)}}{x} } = {\lim\limits_{x \to \pm \infty } \frac{{x + \arctan x}}{x} } = {\lim\limits_{x \to \pm \infty } \left( {1 + \frac{{\arctan x}}{x}} \right) } = {1 + \lim\limits_{x \to \pm \infty } \frac{{\arctan x}}{x}.} \] Функция арктангенс ограничена в интервале \(\left( { - \large\frac{\pi }{2}\normalsize,\large\frac{\pi }{2}\normalsize} \right)\). Поэтому в последнем выражении предел при \(x \to \pm \infty\) равен нулю. Следовательно, \(k = 1,\) причем это значение одинаково при стремлении к плюс- или минус-бесконечности. Вычислим коэффициент \(b\) отдельно для случая \(x \to -\infty\) и \(x \to +\infty:\) \[ {{b_1} = \lim\limits_{x \to - \infty } \left[ {y\left( x \right) - kx} \right] } = {\lim\limits_{x \to - \infty } \left[ {\cancel{x} + \arctan x - \cancel{x}} \right] } = {\lim\limits_{x \to - \infty } \arctan x } = { - \frac{\pi }{2},} \] \[ {{b_2} = \lim\limits_{x \to + \infty } \left[ {y\left( x \right) - kx} \right] } = {\lim\limits_{x \to + \infty } \arctan x } = { + \frac{\pi }{2}.} \] Таким образом, найдено две наклонных асимптоты (одна для случая \(x \to -\infty\) и другая для \(x \to +\infty\)). Их уравнения имеют такой вид: \[ {x \to - \infty :\;\;y = kx + {b_1} } = {x - \frac{\pi }{2},} \] \[ {x \to + \infty :\;\;y = kx + {b_2} } = {x + \frac{\pi }{2}.} \] Схематический вид функции и ее асимптот показан на рисунке \(7.\)
|
||||||||||||
|
Пример 5
|
||||||||||||
|
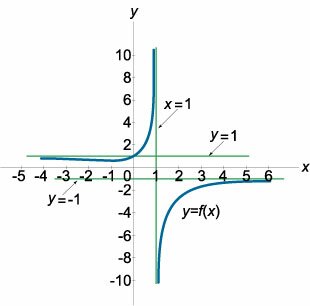
Найти асимптоты графика функции \[y = \frac{{\sqrt {1 + {x^2}} }}{{x - 1}}.\]
Решение.
Функция имеет разрыв второго рода при \(x = 1.\) Так как \[ {\lim\limits_{x \to 1 - 0} y\left( x \right) } = {\lim\limits_{x \to 1 - 0} \frac{{\sqrt {1 + {x^2}} }}{{x - 1}} } = {\frac{{\sqrt {1 + {{\left( {1 - 0} \right)}^2}} }}{{\left( {1 - 0} \right) - 1}} } = {\frac{{\sqrt 2 }}{{ - 0}} = - \infty ,} \] \[ {\lim\limits_{x \to 1 + 0} y\left( x \right) } = {\lim\limits_{x \to 1 + 0} \frac{{\sqrt {1 + {x^2}} }}{{x - 1}} } = {\frac{{\sqrt {1 + {{\left( {1 + 0} \right)}^2}} }}{{\left( {1 + 0} \right) - 1}} } = {\frac{{\sqrt 2 }}{{ + 0}} = + \infty,} \] то \(x = 1\) является вертикальной асимптотой.Поскольку порядок роста числителя и знаменателя одинаков, то график имеет также горизонтальную асимптоту. В пределе при \(x \to +\infty\) получаем \[ {\lim\limits_{x \to + \infty } y\left( x \right) } = {\lim\limits_{x \to + \infty } \frac{{\sqrt {1 + {x^2}} }}{{x - 1}} } = {\lim\limits_{x \to + \infty } \sqrt {\frac{{1 + {x^2}}}{{{{\left( {x - 1} \right)}^2}}}} } = {\lim\limits_{x \to + \infty } \sqrt {\frac{{1 + {x^2}}}{{{x^2} - 2x + 1}}} } = {\lim\limits_{x \to + \infty } \sqrt {\frac{{\frac{1}{{{x^2}}} + 1}}{{1 - \frac{2}{x} + \frac{1}{{{x^2}}}}}} } = {\frac{1}{1} = 1.} \] Аналогично, предел функции при \(x \to -\infty\) равен \[ {\lim\limits_{x \to - \infty } y\left( x \right) } = {\lim\limits_{x \to - \infty } \frac{{\sqrt {1 + {x^2}} }}{{x - 1}} } = {\lim\limits_{x \to - \infty } \frac{{\sqrt {1 + {x^2}} }}{{\left( { - \sqrt {{{\left( {x - 1} \right)}^2}} } \right)}} } = { - \lim\limits_{x \to - \infty } \sqrt {\frac{{1 + {x^2}}}{{{x^2} - 2x + 1}}} } = { - \lim\limits_{x \to - \infty } \sqrt {\frac{{\frac{1}{{{x^2}}} + 1}}{{1 - \frac{2}{x} + \frac{1}{{{x^2}}}}}} } = { - \frac{1}{1} = - 1.} \] Таким образом, при \(x \to +\infty\) график функции имеет горизонтальную асимптоту \(y = 1,\) а при \(x \to -\infty\) − асимптоту \(y = -1.\) Схематически график функции показан на рисунке \(8.\) |
||||||||||||
|
Пример 6
|
||||||||||||
|
Найти асимптоты линии, заданной параметрическими уравнениями \[ {x = \varphi \left( t \right) = \frac{1}{{t - 2}},}\;\;\; {y = \psi \left( t \right) = \frac{t}{{t - 1}}.} \]
Решение.
Исследуем точку \(t = 2.\) Вычислим пределы функций \(x = \varphi \left( t \right)\) и \(y = \psi \left( t \right)\) при \(t \to 2:\) \[ {\lim\limits_{t \to 2} \varphi \left( t \right) } = {\lim\limits_{t \to 2} \frac{1}{{t - 2}} = \infty ,}\;\;\; {\lim\limits_{t \to 2} \psi \left( t \right) } = {\lim\limits_{t \to 2} \frac{t}{{t - 1}} = 2.} \] Итак, при \(t \to 2\) координата \(x\) стремится к бесконечности, а координата \(y\) − к конечному значению \(y = 2.\) Следовательно, в этой точке существует горизонтальная асимптота \(y = 2.\)Аналогично рассмотрим точку \(t = 1,\) в которой терпит разрыв функция \(y\left( t \right):\) \[ {\lim\limits_{t \to 1} \varphi \left( t \right) } = {\lim\limits_{t \to 1} \frac{1}{{t - 2}} = -1,}\;\;\; {\lim\limits_{t \to 1} \psi \left( t \right) } = {\lim\limits_{t \to 1} \frac{t}{{t - 1}} = \infty.} \] Здесь мы имеем вертикальную асимптоту \(x = -1.\) Из вида функции \(x = \varphi \left( t \right)\) следует, что \(t = 2\) − единственное значение параметра \(t,\) при котором координата \(x\) стремится к бесконечности. Отсюда следует, что кривая не имеет наклонных асимптот. Итак, данная кривая имеет горизонтальную асимптоту \(y = 2\) и вертикальную асимптоту \(x = -1.\) Ее схематический вид представлен на рисунке \(9.\)
|
||||||||||||
|
Пример 7
|
||||||||||||
|
Найти асимптоты линии, заданной параметрическими уравнениями \[ {x = \varphi \left( t \right) = \frac{t}{{1 - {t^2}}},}\;\;\; {y = \psi \left( t \right) = \frac{{{t^2}}}{{1 - {t^2}}}.} \]
Решение.
При \(t = \pm 1\) знаменатели в выражениях для \(x\) и \(y\) равны нулю. Поэтому при этих значениях \(t\) имеем: \[ {\lim\limits_{t \to \pm 1} \varphi \left( t \right) = \lim\limits_{t \to \pm 1} \frac{t}{{1 - {t^2}}} = \infty ,}\;\;\; {\lim\limits_{t \to \pm 1} \psi \left( t \right) = \lim\limits_{t \to \pm 1} \frac{{{t^2}}}{{1 - {t^2}}} = \infty .} \] Следовательно, при \(t = -1\) и \(t = 1\) могут существовать наклонные асимптоты. Исследуем сначала точку \(t = -1:\) \[ {{k_1} = \lim\limits_{t \to - 1} \frac{{\psi \left( t \right)}}{{\varphi \left( t \right)}} } = {\lim\limits_{t \to - 1} \frac{{\frac{{{t^2}}}{{1 - {t^2}}}}}{{\frac{t}{{1 - {t^2}}}}} } = {\lim\limits_{t \to - 1} \frac{{{t^2}}}{t} } = {\lim\limits_{t \to - 1} t = - 1,} \] \[ {{b_1} = \lim\limits_{t \to - 1} \left[ {\psi \left( t \right) - {k_1}\varphi \left( t \right)} \right] } = {\lim\limits_{t \to - 1} \left[ {\frac{{{t^2}}}{{1 - {t^2}}} - \left( { - 1} \right)\frac{t}{{1 - {t^2}}}} \right] } = {\lim\limits_{t \to - 1} \frac{{{t^2} + t}}{{1 - {t^2}}} } = {\lim\limits_{t \to - 1} \frac{{t\cancel{\left( {t + 1} \right)}}}{{\left( {1 - t} \right)\cancel{\left( {1 + t} \right)}}} } = {\lim\limits_{t \to - 1} \frac{t}{{1 - t}} = - \frac{1}{2}.} \] Таким образом, при \(t = -1\) существует наклонная асимптота, уравнение которой имеет вид: \[y = {k_1}x + {b_1} = - x - \frac{1}{2}.\] Аналогично найдем уравнение асимптоты в точке \(t = 1:\) \[ {{k_2} = \lim\limits_{t \to 1} \frac{{\psi \left( t \right)}}{{\varphi \left( t \right)}} } = {\lim\limits_{t \to 1} \frac{{\frac{{{t^2}}}{{1 - {t^2}}}}}{{\frac{t}{{1 - {t^2}}}}} } = {\lim\limits_{t \to 1} \frac{{{t^2}}}{t} } = {\lim\limits_{t \to 1} t = 1,} \] \[ {{b_2} = \lim\limits_{t \to 1} \left[ {\psi \left( t \right) - {k_2}\varphi \left( t \right)} \right] } = {\lim\limits_{t \to 1} \left[ {\frac{{{t^2}}}{{1 - {t^2}}} - \frac{t}{{1 - {t^2}}}} \right] } = {\lim\limits_{t \to 1} \frac{{{t^2} - t}}{{1 - {t^2}}} } = {\lim\limits_{t \to 1} \frac{{t\left( {t - 1} \right)}}{{\left( {1 - t} \right)\left( {1 + t} \right)}} } = { - \lim\limits_{t \to 1} \frac{t}{{1 + t}} = - \frac{1}{2}.} \] Итак, в указанной точке существует асимптота. Ее уравнение записывается как \[y = {k_2}x + {b_2} = x - \frac{1}{2}.\] Других значений \(t\), при которых координаты \(x\) и \(y\) стремятся в бесконечность, не существует. Следовательно, у кривой нет других асимптот.Данная линия состоит из двух ветвей, причем нижняя ветвь не определена при \(x = 0\) (когда \(t \to \pm\infty\)). Вид кривой показан схематически на рисунке \(10.\) |
||||||||||||
|
Пример 8
|
||||||||||||
|
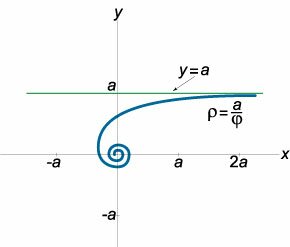
Найти асимптоты гиперболической спирали, заданной уравнением \(\rho = \large\frac{a}{\varphi }\normalsize.\)
Решение.
Выразим угол \(\varphi\) через радиус \(\rho:\) \[\varphi = \frac{a}{\rho }.\] Асимптота в полярных координатах определяется параметрами \(\alpha\) и \(p\). Вычислим сначала угол \(\alpha:\) \[ {\alpha = \lim\limits_{\rho \to \infty } \varphi } = {\lim\limits_{\rho \to \infty } \frac{a}{\rho } = 0,} \] т.е. асимптота (если она существует) расположена горизонтально. Определим параметр \(p:\) \[ {p = \lim\limits_{\rho \to \infty } \left[ {\rho \sin \left( {\alpha - \varphi } \right)} \right] } = {\lim\limits_{\rho \to \infty } \left[ {\rho \sin \left( {0 - \varphi } \right)} \right] } = { - \lim\limits_{\rho \to \infty } \left( {\rho \sin \varphi } \right) } = { - \lim\limits_{\rho \to \infty } \left( {\rho \sin \frac{a}{\rho }} \right) } = { - \lim\limits_{\rho \to \infty } \frac{{\sin \frac{a}{\rho }}}{{\frac{1}{\rho }}} } = { - \lim\limits_{\frac{a}{\rho } \to 0} \frac{{a\sin \frac{a}{\rho }}}{{\frac{a}{\rho }}} } = { - a\lim\limits_{\frac{a}{\rho } \to 0} \frac{{\sin \frac{a}{\rho }}}{{\frac{a}{\rho }}} } = { - a \cdot 1 = - a.} \] Здесь мы учли, что первый замечательный предел равен \(1.\)Следовательно, у гиперболической спирали существует горизонтальная асимптота с параметрами \(\alpha =0\), \(p = -a.\) В декартовых координатах ее уравнение имеет вид \(y = a\) (рисунок \(11\)).
|
||||||||||||
|
Пример 9
|
||||||||||||
|
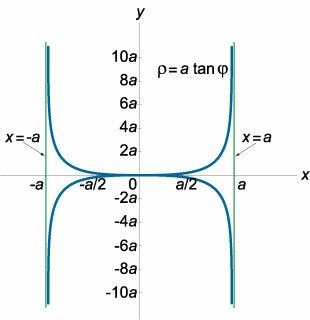
Найти асимптоты кривой, заданной в полярных координатах: \[\rho = a\tan \varphi .\]
Решение.
Выразим из уравнения обратную зависимость \(\varphi \left( \rho \right):\) \[ {\rho = a\tan \varphi ,}\;\; {\Rightarrow \frac{\rho }{a} = \tan \varphi ,}\;\; {\Rightarrow \varphi = \arctan \frac{\rho }{a}.} \] Асимптота в полярных координатах определяется двумя параметрами: углом \(\alpha\) и расстоянием \(p\) от центра до асимптоты. Угол \(\alpha\) вычисляется по формуле: \[ {\alpha = \lim\limits_{\rho \to \infty } \varphi } = {\lim\limits_{\rho \to \infty } \arctan \frac{\rho }{a} } = {\lim\limits_{\frac{\rho }{a} \to \infty } \arctan \frac{\rho }{a} } = {\frac{\pi }{2}.} \] Параметр \(p\), соответственно, равен: \[ {p = \lim\limits_{\rho \to \infty } \left[ {\rho \sin \left( {\alpha - \varphi } \right)} \right] } = {\lim\limits_{\rho \to \infty } \left[ {\rho \sin \left( {\frac{\pi }{2} - \varphi } \right)} \right] } = {\lim\limits_{\rho \to \infty } \left[ {\rho \cos \varphi } \right] } = {\lim\limits_{\rho \to \infty } \left[ {\rho \cos \left( {\arctan \frac{\rho }{a}} \right)} \right].} \] Используем далее следующее соотношение: \[\arctan z = \arccos \frac{1}{{\sqrt {1 + {z^2}} }}.\] Тогда \[ {\rho \cos \left( {\arctan \frac{\rho }{a}} \right) } = {\rho \cos \left( {\arccos \frac{1}{{\sqrt {1 + {{\left( {\frac{\rho }{a}} \right)}^2}} }}} \right) } = {\rho \cos \left( {\arccos \sqrt {\frac{{{a^2}}}{{{a^2} + {\rho ^2}}}} } \right) } = { \pm \frac{{\rho a}}{{\sqrt {{a^2} + {\rho ^2}} }}.} \] Следовательно, параметр \(p\) равен: \[ {p = \lim\limits_{\rho \to \infty } \left( { \pm \frac{{\rho a}}{{\sqrt {{a^2} + {\rho ^2}} }}} \right) } = { \pm \lim\limits_{\rho \to \infty } \frac{a}{{\sqrt {\frac{{{a^2}}}{{{\rho ^2}}} + 1} }} = \pm a.} \] Итак, мы получили два значения параметра \(p:\) \(p = +a\) и \(p = -a,\) т.е. существуют две асимптоты. Поскольку угол \(\alpha\) у обеих асимптот одинаков и равен \(\large\frac{\pi }{2}\normalsize,\) то обе асимптоты являются вертикальными. В таком случае \(p\) − это расстояние от центра до асимптоты вдоль оси \(x.\) Тогда в декартовых координатах уравнения асимптот выглядят как \(x = a\) и \(x = -a.\) Схематически это изображено на рисунке \(12.\) |
||||||||||||
|
Пример 10
|
||||||||||||
|
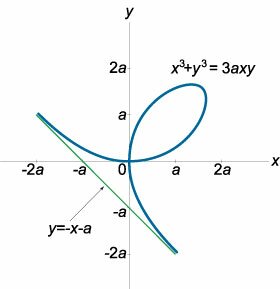
Найти асимптоты декартова листа, заданного уравнением \[{x^3} + {y^3} = 3axy.\]
Решение.
Исследуем сначала наклонные асимптоты данной кривой. Запишем неявное уравнение в виде \[{x^3} + {y^3} - 3axy = 0.\] Подставляя уравнение асимптоты \(y =kx + b,\) получаем: \[ {{x^3} + {\left( {kx + b} \right)^3} - 3ax\left( {kx + b} \right) = 0,}\;\; {\Rightarrow {x^3} + {k^3}{x^3} + 3{k^2}b{x^2} + 3k{b^2}x + {b^3} - 3ak{x^2} - 3abx = 0,}\;\; {\Rightarrow \left( {1 + {k^2}} \right){x^3} + \left( {3{k^2}b - 3ak} \right){x^2} + \left( {3k{b^2} - 3ab} \right)x + {b^3} = 0.} \] Приравнивая коэффициенты при двух старших членах нулю, находим параметры асимптоты \(k\) и \(b:\) \[ {\left\{ \begin{array}{l} 1 + {k^3} = 0\\ 3{k^2}b - 3ak = 0 \end{array} \right.,}\;\; {\Rightarrow \left\{ \begin{array}{l} {k^3} = - 1\\ 3k\left( {kb - a} \right) = 0 \end{array} \right.,}\;\; {\Rightarrow k = - 1,}\;\; {\Rightarrow - b - a = 0,}\;\; {\Rightarrow b = - a.} \] Таким образом, декартов лист имеет наклонную асимптоту (рисунок \(13\)), которая описывается уравнением \(y = -x -a.\)Проверим возможность существования вертикальной асимптоты. Пусть ее уравнение записывается как \(y = c.\) Подставим это в исходное неявное уравнение кривой: \[ {{x^3} + {y^3} - 3axy = 0,}\;\; {\Rightarrow {c^3} + {y^3} - 3acy = 0,}\;\; {\Rightarrow {y^3} - 3acy + {c^3} = 0.} \] Заметим, что в последнем равенстве присутствует слагаемое в старшей степени \({y^3}.\) Это означает, что необходимое условие существования вертикальной асимптоты не выполняется. Следовательно, декартов лист имеет лишь наклонную асимптоту, найденную выше.
|
||||||||||||
|
Пример 11
|
||||||||||||
|
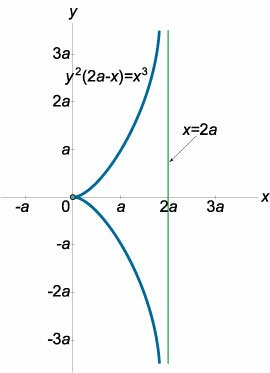
Найти асимптоты циссоиды Диокла, заданной уравнением \[{y^2}\left( {2a - x} \right) = {x^3},\;\;a > 0.\]
Решение.
Исследуем наклонные асимптоты. Подставим \(y = kx + b\) в заданное уравнение: \[ {{y^2}\left( {2a - x} \right) = {x^3},}\;\; {\Rightarrow {\left( {kx + b} \right)^2}\left( {2a - x} \right) = {x^3},}\;\; {\Rightarrow \left( {{k^2}{x^2} + 2kbx + {b^2}} \right)\left( {2a - x} \right) = {x^3},}\;\; {\Rightarrow \color{red}{2a{k^2}{x^2}} + \color{green}{4akbx} + 2a{b^2} - \color{blue}{{k^2}{x^3}} - \color{red}{2kb{x^2}} - \color{green}{{b^2}x} - \color{blue}{x^3} = 0,}\;\; {\Rightarrow \color{blue}{\left( { - {k^2} - 1} \right){x^3}} + \color{red}{\left( {2a{k^2} - 2kb} \right){x^2}} + \color{green}{\left( {4akb - {b^2}} \right)x} + 2a{b^2} = 0.} \] Параметры \(k\) и \(b\) наклонной асимптоты определяются из условия \[\left\{ \begin{array}{l} - {k^2} - 1 = 0\\ 2a{k^2} - 2kb = 0 \end{array} \right..\] Однако из первого уравнения видно, что \(k\) не имеет действительных решений: \[ {- {k^2} - 1 = 0,}\;\; {\Rightarrow {k^2} = - 1,}\;\; {\Rightarrow k \in \emptyset .} \] Следовательно, наклонной асимптоты у циссоиды не существует.Рассмотрим вертикальную асимптоту. Подставляя \(x = c\) в исходное уравнение, получаем: \[ {{y^2}\left( {2a - c} \right) = {c^3}}\;\;\;\text{или}\;\;\; {\left( {2a - c} \right){y^2} - {c^3} = 0.} \] Заметим, что циссоида является кривой третьего порядка. При этом в последнем соотношении отсутствует член третьей степени. В таком случае вертикальная асимптота существует и ее параметр \(с\) определяется из условия \[2a - c = 0,\;\; \Rightarrow c = 2a.\] Итак, циссоида Диокла имеет одну вертикальную асимптоту \(x = 2a\) (рисунок \(14\)). Замечание. Уравнение циссоиды допускает запись в явной форме: \[ {{y^2}\left( {2a - x} \right) = {x^3},}\;\; {\Rightarrow {y^2} = \frac{{{x^3}}}{{2a - x}},}\;\; {\Rightarrow y = \pm \sqrt {\frac{{{x^3}}}{{2a - x}}},} \] откуда сразу следует, что в точке \(x = 2a\) существует разрыв второго рода, и следовательно, прямая \(x = 2a\) является вертикальной асимптотой. |
||||||||||||
|
Пример 12
|
||||||||||||
|
Доказать, что функции \[ {f\left( x \right) = \sqrt {{x^2} + 4x + 3} \;\;\;\text{и}}\;\; {g\left( x \right) = \frac{{{x^3} + 2{x^2}}}{{{x^2} + 1}}} \] асимптотически равны друг другу при \(x \to +\infty.\) Вычислить погрешность приближенного равенства \(f\left( {100} \right) \approx g\left( {100} \right).\)
Решение. |
||||||||||||